dimanche 16 juillet 2006
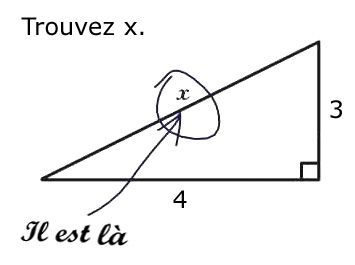
Trouvez x !
Par Didier MÞller, dimanche 16 juillet 2006 à 11:00 - Humour/bÊtisier
lu 9584 fois
Ce blog a pour sujet les mathématiques et leur enseignement
au Lycée. Son but est triple.
Premièrement, ce blog est pour moi une manière idéale de
classer les informations que je glâne au cours de mes voyages en Cybérie.
Deuxièmement, ces billets me semblent bien adaptés à la
génération zapping de nos élèves. Ces textes courts
et ces vidéos, privilégiant le côté ludique des maths,
pourront, je l'espère, les intéresser et leur donner l'envie d'en
savoir plus.
Enfin, c'est un bon moyen de communiquer avec des collègues de toute
la francophonie.
dimanche 16 juillet 2006
Par Didier MÞller, dimanche 16 juillet 2006 à 11:00 - Humour/bÊtisier

lu 9584 fois
samedi 15 juillet 2006
Par Didier MÞller, samedi 15 juillet 2006 à 10:24 - Logiciels/applets/IA
IntÃĐgramme est un utilitaire gratuit qui vous aide à la rÃĐsolution des casse-tÊte du style : Paul a 2 ans de plus que celui qui a la voiture rouge et 4 de moins que le vendeur.
lu 8169 fois
vendredi 14 juillet 2006
Par Didier MÞller, vendredi 14 juillet 2006 à 08:18 - Livres/e-books

Comme tout le monde, j'ai mes petites habitudes: chaque mois je passe à la bibliothÃĻque du LycÃĐe pour lire la chronique toujours claire et intÃĐressante de Jean-Paul Delahaye dans la rubrique "Logique et calcul" de la revue Pour la Science. PÃĐriodiquement, les ÃĐditions Belin sortent une compilation de ses textes sur un thÃĻme donnÃĐ. Il y a dÃĐjà eu entre autres "Le facinant nombre pi", "Jeux mathÃĐmatiques et mathÃĐmatique des jeux", "Merveilleux nombres premiers",... Voici le dernier: "Les inattendus mathÃĐmatiques". Ce livre explore cette frontiÃĻre oÃđ la vie quotidienne, l'art, les jeux, la manipulation des nombres, les figures gÃĐomÃĐtriques et mÊme la philosophie rencontrent les mathÃĐmatiques. Il est dÃĐcoupÃĐ en 5 parties :
lu 6054 fois
jeudi 13 juillet 2006
Par Didier MÞller, jeudi 13 juillet 2006 à 10:39 - Logiciels/applets/IA
Le portail des TIC ntic.org propose un laboratoire virtuel oÃđ l'on trouve des applets pour la physique, l'ÃĐlectricitÃĐ, les mathÃĐmatiques, les probabilitÃĐs et la trigonomÃĐtrie.
lu 6085 fois
mercredi 12 juillet 2006
Par Didier MÞller, mercredi 12 juillet 2006 à 10:54 - Il y a des maths là ?
La formule de Widmark donne le taux d'alcoolÃĐmie :
AlcoolÃĐmie = (grammes d'alcool absorbÃĐs) / (poids en kg x c), oÃđ c vaut 0.6 pour les femmes et 0.7 pour les hommes.
La courbe ci-dessous montre l'ÃĐvolution du taux d'alcoolÃĐmie avec le temps.

lu 11543 fois
mardi 11 juillet 2006
Par Didier MÞller, mardi 11 juillet 2006 à 10:22 - Enigmes/casse-tÊte
Hitori (littÃĐralement "laissez-moi seul") est un jeu logique publiÃĐ pour la premiÃĻre fois dans "Puzzle Communication Nikoli" #29, en mars 1990.
Au dÃĐbut du jeu, chaque cellule d'une grille contient un nombre. Le but est de peindre certaines cellules de sorte qu'il n'y ait pas plusieurs fois le mÊme nombre sur une mÊme ligne ou une mÊme colonne.


lu 19910 fois
lundi 10 juillet 2006
Par Didier MÞller, lundi 10 juillet 2006 à 10:03 - Histoire des maths
Les Mayas utilisaient des glyphes comme symboles numÃĐriques. Ces glyphes reprÃĐsentaient des tÊtes de divinitÃĐ vues de profil. Seuls les chiffres allant de zÃĐro à dix-neuf ÃĐtaient ainsi reprÃĐsentÃĐs. Cela s'explique par le fait que les Mayas avaient adoptÃĐ une numÃĐration vigÃĐsimale, c'est-à -dire en base 20.


lu 43569 fois
samedi 8 juillet 2006
Par Didier MÞller, samedi 8 juillet 2006 à 10:11 - Sites de mathÃĐmatiques
On connaÃŪt les critÃĻres de divisibilitÃĐ par 2, 3, 4, 5, 8, 9, 10 et 11. On parle plus rarement du critÃĻre de divisibilitÃĐ par 7 ou 13, qui est commun aux deux nombres.
Soit un nombre N dont on veut tester la divisibilitÃĐ, on le partage en tranches de trois chiffres à partir de la droite. On ajoute et on soustrait alternativement chacune de ces tranches jusquâà ce quâil ne reste plus quâune tranche de trois chiffres. Si ce nombre de trois chiffres est divisible par 7 ou 13, alors le nombre initial lâest. On ramÃĻne ainsi lâexamen de la divisibilitÃĐ par 7 ou 13 de tous les nombres à ceux des nombres de trois chiffres. Il y a encore des calculs à faire, mais ce sont des divisions faciles.
Exemple : 745'857'320.
On mÃĻne lâopÃĐration dÃĐcrite : 745 â 857 + 320 = 208, nombre divisible par 13 (13x16).
Donc le nombre initial lâest, on vÃĐrifie 745'857'320 = 13 * 57'373'640
Cette mÃĐthode fonctionne parce que 1001 est divisible par 7 et par 13.
lu 6727 fois
vendredi 7 juillet 2006
Par Didier MÞller, vendredi 7 juillet 2006 à 09:47 - Citations

Les gens n'aiment pas penser ; c'est qu'ils ont peur de se tromper. Penser, c'est aller d'erreur en erreur. Rien n'est tout à fait vrai. De mÊme aucun chant n'est tout à fait juste. Ce qui fait que la mathÃĐmatique est une ÃĐpreuve redoutable, c'est qu'elle ne console point de l'erreur. ThalÃĻs, Pythagore, ArchimÃĻde ne nous ont point contÃĐ leurs erreurs ; nous n'avons pas connu leurs faux raisonnements ; et c'est bien dommage.
Alain (de son vrai nom Emile Chartier)
lu 5934 fois
jeudi 6 juillet 2006
Par Didier MÞller, jeudi 6 juillet 2006 à 10:06 - Articles/revues
Plus magazine tries to open a window to the world of maths, with all its beauty and applications, by providing articles from the top mathematicians and science writers on topics as diverse as art, medicine, cosmology and sport.
lu 5663 fois
mercredi 5 juillet 2006
Par Didier MÞller, mercredi 5 juillet 2006 à 08:44 - Cours en ligne/MOOC
Labomath est un cours de math en ligne comme je les aime : beaucoup d'interactivitÃĐ (applet java, QCM, exercices d'oral de bac), des ressources, et, bien sÃŧr, un cours au format OpenOffice.
lu 6344 fois
mardi 4 juillet 2006
Par Didier MÞller, mardi 4 juillet 2006 à 10:13 - Insolite
Faire ÃĐteindre leurs tÃĐlÃĐphones portables à une classe d'adolescents n'est pas une mince affaire, notamment lorsque ces derniers ont trouvÃĐ une sonnerie inaudible pour les adultes. Dans les endroits oÃđ les portables doivent rester ÃĐteints, les moins de 20 ans on trouvÃĐ une parade : la mosquitotone, aussi connue sous le nom de teen buzz.
Tout a commencÃĐ lorsqu'une entreprise a mis au point une sonnerie destinÃĐe à ÃĐloigner les ados qui se regroupent devant des magasins sans pour autant dÃĐranger les adultes. Sur quel mÃĐcanisme se base ce son ? Il semblerait qu'en grandissant, les adultes voient leurs capacitÃĐs auditives s'amoindrir et qu'ils n'entendent plus certaines franges de sons. C'est bien cette faiblesse qui est exploitÃĐe par le Mosquito.
Ce principe a ÃĐtÃĐ inversÃĐ par les adolescents qui se sont dits qu'ils pouvaient le retourner en leur faveur en l'utilisant comme sonnerie de portable. Le Mosquito est devenu Mosquitotone (sonnerie Mosquito) et a fait fureur auprÃĻs des adolescents amÃĐricains puis anglais. Il a aussi ÃĐtÃĐ imitÃĐ par d'autres firmes qui veulent profiter de son potentiel.
Cependant, il semble que certains adultes entendent mieux que d'autres et que ceux-là ne soient donc pas dupes puisqu'ils entendent les ultra-sons en question. Faites le test !
lu 7757 fois
lundi 3 juillet 2006
Par Didier MÞller, lundi 3 juillet 2006 à 09:38 - Cours en ligne/MOOC
Etranger du collÃĻge, du lycÃĐe ou de l'universitÃĐ, le tenancier de la taverne de l'Irlandais te propose un vaste choix de cours de maths interactifs avec des tests de connaissances et des outils interactifs.
lu 7841 fois
dimanche 2 juillet 2006
Par Didier MÞller, dimanche 2 juillet 2006 à 08:31 - Logiciels/applets/IA
J/link est une technologie qui permet de lier Java et Mathematica. Le site J/Link Applications Site de Hidekazu Takahashi montre des applications possibles.
lu 6121 fois
vendredi 30 juin 2006
Par Didier MÞller, vendredi 30 juin 2006 à 10:59 - Enigmes/casse-tÊte
Jeffrey Shep propose des dizaines d'ÃĐnigmes sur son site. De quoi passer le temps pendant les vacances, au cas oÃđ vous ne sauriez pas quoi faire. Ce n'est pas du tout mon cas. J'espÃĻre au contraire avoir assez de temps pour faire tout ce que j'ai prÃĐvu!
Bravo aux nouveaux bacheliers et diplÃīmÃĐs du Jura!
lu 6615 fois
jeudi 29 juin 2006
Par Didier MÞller, jeudi 29 juin 2006 à 12:49 - Sites de mathÃĐmatiques
MATHS-ROMETUS, MathÃĐmatiques accessibles à tous : On y trouve l'histoire des maths en images, tout ce qui peut rimer avec les mathÃĐmatiques (les nombres et les opÃĐrations, leur histoire, la numÃĐrologie, la littÃĐrature, l'ÃĐtymologie, les jeux , les figures au compas, les polyÃĻdres, le pourquoi et lâintÃĐrÊt, la magie, un dictionnaire, etc.), les mathÃĐmatiques au collÃĻge et les 25 productions de lâauteur, Jean-luc ROMET.
lu 7868 fois
mardi 27 juin 2006
Par Didier MÞller, mardi 27 juin 2006 à 10:20 - Enigmes/casse-tÊte
 Enigmes mathÃĐmatiques diaboliques est un petit livre qui regroupe 65 ÃĐnigmes mathÃĐmatiques classiques, avec leur solution. On retrouve ces ÃĐnigmes sur le site de l'auteur: www.bric-a-brac.org/enigmes/.Personnellement, j'en connaissais une bonne moitiÃĐ, mais il y en a une ou deux qui sont vraiment pas mal. Par exemple, presque tout le monde connait la fameuse suite :
Enigmes mathÃĐmatiques diaboliques est un petit livre qui regroupe 65 ÃĐnigmes mathÃĐmatiques classiques, avec leur solution. On retrouve ces ÃĐnigmes sur le site de l'auteur: www.bric-a-brac.org/enigmes/.Personnellement, j'en connaissais une bonne moitiÃĐ, mais il y en a une ou deux qui sont vraiment pas mal. Par exemple, presque tout le monde connait la fameuse suite :
1
11
21
1211
111221
312211
...
Mais sauriez-vous dÃĐmontrer que le chiffre 4 ne peut jamais apparaÃŪtre dans cette suite ?
lu 16717 fois
lundi 26 juin 2006
Par Didier MÞller, lundi 26 juin 2006 à 07:43 - Livres/e-books

Voilà Un petit livre vraiment pas cher (2 Euros) qui rÃĐsume assez bien ce qu'il faut savoir avant d'entrer au lycÃĐe : aires de polygones, conversions d'unitÃĐs, pourcentages, rÃĻgle de trois, vitesse, thÃĐorÃĻme de ThalÃĻs, ... Chaque chapitre traite d'un problÃĻme pratique: combien de pots de peinture acheter pour repeindre un mur, mesurer une distance sur une carte de gÃĐographie, etc. Mon seul reproche concerne le titre: le mot magique n'a rien à y faire.
Langue: Français Ãditeur : J'ai Lu (12 mai 2006)
Collection : Librio MÃĐmo
Format : Poche - 92 pages
ISBN : 2290352225
Dimensions (en cm) : 14 x 1 x 21
lu 8669 fois
dimanche 25 juin 2006
Par Didier MÞller, dimanche 25 juin 2006 à 09:42 - Doc/sÃĐries/films/vidÃĐos
La chaÃŪne de tÃĐlÃĐvision PlanÃĻte propose depuis quelques semaines une sÃĐrie documentaire intitulÃĐe "Les voyous du casino". Cette sÃĐrie raconte le parcours - incroyable mais vrai - dâas de lâarnaque et de petits gÃĐnies en mathÃĐmatiques qui ont rÃĐussi à mettre au point des mÃĐthodes plus ou moins lÃĐgales pour gagner des sommes folles au casino. Certains ont profitÃĐ de leur fortune, dâautres se sont retrouvÃĐs derriÃĻre les barreaux, mais tous ont vÃĐcu des moments palpitants.
L'ÃĐpisode "Les deux font la paire" est consacrÃĐ Ã Edward Thorp, jeune docteur en mathÃĐmatique, qui va dÃĐmontrer que gagner au blackjack n'est pas une simple question de chance. AccompagnÃĐ de son financier, Manny Kimmel, il va parcourir le monde des casinos et devenir riche. En 1959, Eddy Thorp dÃĐcouvre un article sur le blackjack. A partir de là , le jeune docteur en mathÃĐmatique va s'intÃĐresser à ce jeu. Au bout de deux ans, à force de statistiques, il trouve un systÃĻme de comptage qui permet de vaincre les tables de blackjack. GrÃĒce à son systÃĻme, Eddy Thorp devient une cÃĐlÃĐbritÃĐ mÃĐdiatique, mais de nombreux mathÃĐmaticiens le mettent en doute. Le seul moyen de prouver l'efficacitÃĐ de sa technique est de la tester dans un casino. Pour cela, il a besoin de 10 000 dollars. Or il ne les a pas. C'est alors qu'il rencontre le riche Manny Kimmel, un parieur capable de miser sur n'importe quoi. Les deux hommes s'entraÃŪnent pendant six semaines d'affilÃĐe, au bout desquelles ils s'envolent pour Reno (Nevada). Pari gagnÃĐ. Son systÃĻme de comptage marche ! Eddy va donc enchaÃŪner les casinos. Plus il gagne, plus les casinos le remarquent. Il finit par Être interdit de jeu partout. Le comptage des cartes est nÃĐ. Eddy Thorp va mÊme raconter son aventure dans un livre ("Beat the Dealer", encore disponible aujourd'hui) qui sera en rÃĐalitÃĐ un manuel d'instruction de sa mÃĐthode. Celui-ci va remporter un immense succÃĻs, à la plus grande crainte des directeurs de casinos, qui seront contraints d'augmenter le nombre de talons pour contrecarrer la stratÃĐgie mise au point par Thorp.
A voir : Mathematics gambling: card counting blackjack basic strategy
lu 10056 fois
samedi 24 juin 2006
Par Didier MÞller, samedi 24 juin 2006 à 12:55 - Insolite
Deux ÃĐtudiants ont mis à profit l'intelligence artificielle pour dÃĐterminer que le BrÃĐsil gagnera la Coupe du monde de football. Imran Fanaswala et Yashar Fasihnia, deux ÃĐtudiants en informatique aux Ãmirats arabes unis, ont mis au point un programme informatique baptisÃĐ FIFI pour ÂŦFifa IntelligenceÂŧ. Les deux jeunes hommes de 22 ans ont utilisÃĐ des notions de statistique pour mettre au point leur ÂŦprÃĐdicteur de Coupe du mondeÂŧ. Ils ont amassÃĐ 20 ans de donnÃĐes et d'informations sur les diverses ÃĐquipes: performance, nombre de buts, marqueurs, etc. Le professeur Joachim Diederich qui a supervisÃĐ le projet affirme que FIFI a un taux de prÃĐcision de 83%. FIFI prÃĐvoit donc que le BrÃĐsil gagnera contre l'Angleterre lors des demi-finales et que l'Italie ÃĐliminera les Pays-Bas. Et selon le programme d'Irman et Yashar, le BrÃĐsil l'emportera en finale contre l'Italie.
L'Italie ÃĐliminera les Pays-Bas, ce n'est plus possible, puisque ces deux pays ne sont pas dans la mÊme partie du tableau. Par contre, les autres pronostics sont encore possibles.
lu 8244 fois
< 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 >