vendredi 15 dÃĐcembre 2006
Par Didier MÞller,
vendredi 15 dÃĐcembre 2006 à 09:27
- Articles/revues
IntÃĐressant article de Jean-Paul Delahaye dans le numÃĐro 360 de la revue Pour la Science (dÃĐcembre 2006) sur le lemme de Burnside (qui n'est d'ailleurs pas de lui). Ce lemme est utile pour le dÃĐnombrement, par exemple pour calculer le nombre de façons diffÃĐrentes de colorier les faces d'un cube avec k couleurs. Et comme toujours, l'auteur prÃĐsente ce lemme de maniÃĻre comprÃĐhensible!
A voir : Wikipedia : Burnside's lemma et Applying Burnside's lemma to a one-dimensional Escher Problem
lu 6498 fois
jeudi 14 dÃĐcembre 2006
Par Didier MÞller,
jeudi 14 dÃĐcembre 2006 à 11:43
- Citations

Les schÃĐmas du mathÃĐmaticiens, comme ceux du peintre ou du poÃĻte, doivent Être beaux ; les idÃĐes, comme les couleurs ou les mots, doivent s'assembler de façon harmonieuse. La beautÃĐ est le premier test : il n'y a pas de place durable dans le monde pour les mathÃĐmatiques laides.
Godfrey Harold Hardy (1877-1947)
lu 7877 fois
mardi 12 dÃĐcembre 2006
Par Didier MÞller,
mardi 12 dÃĐcembre 2006 à 08:29
- Jeux / ThÃĐorie des jeux
 Parmi tous les tours de magie, il existe un ensemble particulier, celui des "tours de cartes automatiques". Pouvant Être faits avec un jeu de carte usuel et ne demandant aucune manipulation prÃĐparatoire des cartes, ils sont liÃĐs aux mathÃĐmatiques par des outils simples (symÃĐtrie, comptage, permutations...).
Parmi tous les tours de magie, il existe un ensemble particulier, celui des "tours de cartes automatiques". Pouvant Être faits avec un jeu de carte usuel et ne demandant aucune manipulation prÃĐparatoire des cartes, ils sont liÃĐs aux mathÃĐmatiques par des outils simples (symÃĐtrie, comptage, permutations...).
Arnaud Gazagnes prÃĐsente quelques-uns de ces tours avec leur explication (ce qui permettra aussi bien à l'enseignant qu'à l'ÃĐlÃĻve d'en construire sur le mÊme modÃĻle), et des idÃĐes d'utilisation d'un tableur.
Lire l'article
lu 11737 fois
lundi 11 dÃĐcembre 2006
Par Didier MÞller,
lundi 11 dÃĐcembre 2006 à 10:25
- Livres/e-books

 Les Prix IgNobel : La science qui fait rire... et rÃĐflÃĐchir
Les Prix IgNobel : La science qui fait rire... et rÃĐflÃĐchir
de Marc Abrahams
PrÃĐsentation de l'ÃĐditeur
Les tartines retombent-elles toujours du cÃītÃĐ du beurre ? Pourquoi la musique d'ascenseur protÃĻge-t-elle des rhumes ? Comment calculer vos risques de finir en enfer ? Comment mettre une grenouille en lÃĐvitation ? Les palourdes ont-elles une libido ? Pourquoi la nourriture est-elle inutile ? Toutes ces questions absurdes ont des rÃĐponses 100 % scientifiques. Ces recherches improbables sont rÃĐcompensÃĐes chaque annÃĐe par des Prix Nobel alternatifs, devenus cultes, les Prix IgNobel, dÃĐcernÃĐs par la communautÃĐ scientifique, dans le cadre prestigieux de l'universitÃĐ de Harvard. Bienvenue dans un monde dÃĐlirant, absurde, parfois extrÊme, qui permet de comprendre, en s'amusant, les lois de l'univers. Un livre dÃĐjà traduit en une dizaine de langues.
lu 5213 fois
vendredi 8 dÃĐcembre 2006
Par Didier MÞller,
vendredi 8 dÃĐcembre 2006 à 14:31
- En classe
MathÃĐmatiques sans frontiÃĻres est un concours inter-classes.
- Des classes entiÃĻres de troisiÃĻme et de seconde ou de niveau ÃĐquivalent dans des pays ÃĐtrangers concourent entre elles.
- Une palette d'exercices variÃĐs leur est proposÃĐe (dix en troisiÃĻme et treize en seconde).
- La solution de l'un des exercices doit Être rÃĐdigÃĐe en langue ÃĐtrangÃĻre.
- La classe s'organise pour rÃĐsoudre les exercices en une heure et demie et rend une seule feuille-rÃĐponse pour chacun d'eux.
lu 6727 fois
jeudi 7 dÃĐcembre 2006
Par Didier MÞller,
jeudi 7 dÃĐcembre 2006 à 13:37
- Enigmes/casse-tÊte

Un cavalier se promÃĻne sur un ÃĐchiquier en passant par toutes les cases une seule fois et en finissant son parcours sur la case de dÃĐpart. Combien y a-t-il de tels parcours ? Je suis tombÃĐ Ã la renverse en voyant l'estimation de Cancela et Mordecki : 1,22 x 10
15 !
Lire l'article : Counting Knightâs Tours through the Randomized Warnsdorff Rule, Hector Cancela and Ernesto Mordecki, September 4, 2006
A voir : Knight's Tour Notes,
le cavalier fou
lu 6716 fois
mercredi 6 dÃĐcembre 2006
Par Didier MÞller,
mercredi 6 dÃĐcembre 2006 à 10:35
- ThÃĐorÃĻmes et dÃĐmonstrations
AprÃĻs avoir crÃĐÃĐ un origami, dÃĐplions la feuille de papier.

Soit la suite des angles a
1, a
2, ..., a
2n autour d'un sommet (notons au passage qu'il y a toujours un nombre pair d'angles autour d'un sommet). Lâaddition dâun angle sur deux autour dâun sommet sur le papier dÃĐpliÃĐ est ÃĐgale à 180° :
a1 + a3 + a5 + ... + a2n-1 = 180° ou a2 + a4 + a6 + ... + a2n = 180°
Les applications techniques de l'art de l'origami sont ÃĐgalement trÃĻs nombreuses: la conception de sÃĐcuritÃĐ gonflable, le dÃĐploiement de panneaux solaires de satellite, la fabrication de tÃĐlescopes de grandes dimensions, etc.
A voir : Kawasaki's Theorem,
Origami & math
lu 9389 fois
mardi 5 dÃĐcembre 2006
Par Didier MÞller,
mardi 5 dÃĐcembre 2006 à 09:45
- DrÃīles de statistiques
DiffÃĐrents mythes populaires ont reliÃĐ la taille du pÃĐnis à celle dâautres organes : le nez, les mains ou les pieds. Dans la comÃĐdie "Coup de Foudre à Notting Hill", Julia Roberts demandait ainsi de maniÃĻre ingÃĐnue : "Tu sais ce quâon dit des hommes qui ont des grands pieds?"âĶ Et bien tout comme dans le film, la rÃĐponse nâest certainement pas celle à laquelle vous pourriez vous attendre! Pour ÃĐtablir si ce mythe populaire reposait sur des observations "scientifiquement dÃĐmontrables", deux urologues ont mesurÃĐ la longueur du sexe de 104 hommes dont ils ont ÃĐgalement notÃĐ la pointure et lâÃĒge. Toutes les mensurations ont ÃĐtÃĐ faites sur des sexes au repos mais "ÃĐtirÃĐs". Alors que la vraie taille du pÃĐnis peut uniquement Être dÃĐterminÃĐe en ÃĐrection, les chercheurs indiquent que leur mÃĐthode reste une bonne indication de la longueur. Au terme de leur ÃĐtude, ces amateurs du double-dÃĐcimÃĻtres ont ainsi pu dÃĐterminer que : - La taille moyenne trouvÃĐe fut de 13 cm, mais varie de 6 à 18 cm ; - Les pointures moyennes ÃĐtaient de 9 en taille anglaises, soit 43 en taille europÃĐenne. Mais en ÃĐtudiant lâensemble des donnÃĐes, aucune corrÃĐlation entre les deux mesures nâa pu Être ÃĐtablie. La science a encore frappÃĐ et câest bel et bien un nouveau mythe qui sâeffondre. Source : BJU International, October 2002, vol.90, Issue 6, p. 586
Lire l'article
Notons qu'une autre ÃĐquipe a reçu le prix Ig Nobel 1998 de statistiques pour une recherche similaire: Jerald Bain du Mt. Sinai Hospital de Toronto et Kerry Siminoski de l'universitÃĐ d'Alberta, pour leur ÃĐtude "The Relationship Among Height, Penile Length, and Foot Size."
lu 22166 fois
lundi 4 dÃĐcembre 2006
Par Didier MÞller,
lundi 4 dÃĐcembre 2006 à 10:33
- Logiciels/applets/IA
MAFALDA (Machine spÃĐcialisÃĐe dans la Fabrication de Labyrinthes et de DÃĐdales aux tracÃĐs AlÃĐatoires) permet de crÃĐer des labyrinthes de formes rectangulaires, polygonales ou circulaires, à partir de donnÃĐes entrÃĐes par les Internautes. Elle en calcule automatiquement la solution et enregistre les figures les plus complexes dans une galerie mise à jour en temps rÃĐel. MAFALDA vous propose ÃĐgalemet de parcourir les dÃĐdales crÃĐÃĐs de façon interactive.
lu 5858 fois
dimanche 3 dÃĐcembre 2006
Par Didier MÞller,
dimanche 3 dÃĐcembre 2006 à 17:51
- Livres/e-books

 PrÃĐsentation de l'ÃĐditeur
PrÃĐsentation de l'ÃĐditeur
GalilÃĐe disait "le monde est ÃĐcrit en langage mathÃĐmatique" et en ignorer l'histoire aussi bien que les fondements ne peut Être que prÃĐjudiciable à l'homme moderne. Ce livre a donc ÃĐtÃĐ ÃĐcrit en pensant à tous ceux qui se demandent "à quoi ça sert les maths?" et pour qui la signification profonde de cette discipline est occultÃĐe par sa difficultÃĐ technique. Il s'adresse à toute personne concernÃĐe de prÃĻs ou de loin par les mathÃĐmatiques : mathÃĐmaticiens, physiciens, biologistes, ÃĐconomistes, etc. Vous trouverez donc :
- 150 thÃĻmes d'ÃĐtude, des plus anciens aux plus modernes : musique pythagoricienne, hypothÃĻse de Riemann, prix d'ÃĐquilibre, symÃĐtries en physique, courbes de BÃĐzier, diffraction, optique linÃĐaire, taux d'intÃĐrÊts, loxodromies, croissances de populations, fractales, chaos, transformÃĐe de Fourier, probabilitÃĐs, relativitÃĐ, etc.
- des rappels de cours couvrant l'essentiel des connaissances nÃĐcessaires à l'honnÊte homme et au futur scientifique: mathÃĐmaticien, physicien, biologiste, ÃĐconomiste... ÃĐmaillÃĐs de rappels sur l'histoire des sciences.
- 350 illustrations correspondant à autant de fichiers Excel, Chamois, Maple tÃĐlÃĐchargeables sur le site: http://promenades-mathematiques.net.
lu 6709 fois
samedi 2 dÃĐcembre 2006
Par Didier MÞller,
samedi 2 dÃĐcembre 2006 à 10:13
- Humour/bÊtisier
Les raccourcis et omissions pratiquÃĐs lors d'exposÃĐs sont bien pires que ceux qu'on trouve dans les textes ÃĐcrits. Des recensions humoristiques de ces abus ont plusieurs fois ÃĐtÃĐ proposÃĐes. En voici une, largement inspirÃĐe par celle de la revue Plot (APMEP OrlÃĐans-Tour, n° 86).
- DÃĐmonstration par l'ÃĐvidence : "La dÃĐmonstration est triviale" ; "ImmÃĐdiat à partir des dÃĐfinitions" ; "On obtient sans peine que..." ; "On voit que..."
- DÃĐmonstration par la confiance : "Vous n'avez qu'à essayer, vous verrez, ça marche". Variante : "Je l'ai dÃĐmontrÃĐ hier chez moi, aucune difficultÃĐ."
- DÃĐmonstration par consensus : "Tous ceux qui sont d'accord lÃĻvent la main". Variante encore plus efficace : "Tous ceux qui ne sont pas d'accord lÃĻvent la main."
- DÃĐmonstration par commoditÃĐ dÃĐnommÃĐe "nos dÃĐsirs sont des rÃĐalitÃĐs" : "Ce serait si beau si c'ÃĐtait vrai, donc..." (Redoutablement dangereuse.)
- DÃĐmonstration par nÃĐcessitÃĐ : "Ãa doit Être vrai, sinon toutes les mathÃĐmatiques s'effondreraient." Variante : "Le cas contraire contredirait un rÃĐsultat bien connu qui ne peut pas Être faux." (Peu de travail est nÃĐcessaire pour en tirer une bonne vieille preuve par l'absurde.)
- DÃĐmonstration par plausibilitÃĐ : "Ãa a l'air bon, donc ça doit Être vrai." (TrÃĻs utilisÃĐ pour ÃĐvaluer le rÃĐsultat d'un long calcul ; ne pas en abuser.)
- DÃĐmonstration par intimidation : "Ne soyez pas stupide! Bien sÃŧr que c'est vrai." Variantes du dÃĐbutant : "MÊme un dÃĐbutant sait ça" ; "Vous l'avez vu en sixiÃĻme"." Variante du devoir pour demain : "Ceux qui en doutent feront la dÃĐmonstration pour demain sur une feuille qu'ils me rendront." Variante du tableau : "Si quelqu'un a des doutes, il passe au tableau le dÃĐmontrer."
- DÃĐmonstration par manque de temps : "Il ne me reste pas assez de temps, vous ferez la dÃĐmonstration vous-mÊme."
- DÃĐmonstration par complexitÃĐ : "La dÃĐmonstration est trop compliquÃĐe pour Être donnÃĐe ici." Variantes : "Je ne peux pas vous le faire, car ça fait partie du programme de l'annÃĐe prochaine." "J'ai fait le calcul en 1985, c'est assez pÃĐnible, je n'ai pas envie de le refaire."
- DÃĐmonstration par accident : "Tiens, tiens, qu'avons-nous là ..." (En fait, tout ÃĐtait calculÃĐ par avance pour obtenir le rÃĐsultat prÃĐtendument inattendu.)
- DÃĐmonstration par la dÃĐfinition dite mÃĐthode du postulat d'Euclide : "On le dÃĐfinit comme vrai." (En abuser risque de diminuer l'intÃĐrÊt de votre cours.)
- DÃĐmonstration par la tautologie : "C'est vrai, parce que c'est vrai." (Risque de vous faire perdre du crÃĐdit, mieux vaut utiliser une des autres mÃĐthodes.)
- DÃĐmonstration par rÃĐfÃĐrence : "Comme c'est ÃĐtabli à la page 289 du ..." (Là encore, si vous en abusez, vous viderez votre cours de sa substance.)
- DÃĐmonstration par perte de rÃĐfÃĐrence : "Je sais que j'ai vu la dÃĐmonstration quelque part." (MÊme si c'est du bluff, prÃĐfÃĐrez la mÃĐthode prÃĐcÃĐdente.)
- DÃĐmonstration par manque d'intÃĐrÊt : "Y a-t-il quelqu'un qui souhaite vraiment voir la dÃĐmonstration?" Variante en combinant avec la dÃĐmonstration par complexitÃĐ : "La dÃĐmonstration est longue et pÃĐnible. Est-ce que je la fais?" Variante dite du calcul merdique : "En gÃĐnÃĐral, quand je me lance dans ce calcul, je me plante. On y va?"
- DÃĐmonstration par obstination : "Vous pouvez croire ce que vous voulez, moi je vous dis que c'est vrai." Variante du contre-exemple : "Trouvez-moi un contre-exemple, en attendant je considÃĻre que c'est vrai." (Contraire à la dÃĐontologie la charge de la preuve ne serait pas à celui qui affirme.)
- DÃĐmonstration par analogie : "C'est la mÊme chose que..." ; "Il suffit de s'inspirer de..." "On procÃĻde comme pour..." (Moyen efficace d'obtenir des rÃĐsultats faux : le procÃĐdÃĐ a coÃŧtÃĐ cher à de nombreux mathÃĐmaticiens.)
- DÃĐmonstration par autoritÃĐ : "Borsnbuch l'a dit." Variante dite de l'ascenseur : "J'ai rencontrÃĐ Borsnbuch dans l'ascenseur, et il est d'accord."
- DÃĐmonstration par renvoi multiple : "On conclut en combinant les lemmes 1, 3, 8 et 15 avec le thÃĐorÃĻme 12, puis en utilisant les propositions 7, 9 et 21."
- DÃĐmonstration par appel à l'opinion publique : "Si c'ÃĐtait vrai ça se saurait, donc c'est faux..." (Contrairement aux apparences, ce procÃĐdÃĐ marche bien, car les rÃĐsultats simples qui n'ont pas ÃĐtÃĐ dÃĐmontrÃĐs sont gÃĐnÃĐralement faux.)
lu 8351 fois
vendredi 1 dÃĐcembre 2006
Par Didier MÞller,
vendredi 1 dÃĐcembre 2006 à 08:15
- Insolite
Les femmes doutent facilement de leurs habiletÃĐs mathÃĐmatiques
Stephanie Levitz, Presse canadienne, Vancouver
Il suffit d'expliquer à des femmes qu'il est dans leur nature d'Être moins douÃĐes en mathÃĐmatiques pour influencer nÃĐgativement leur performance dans ce domaine, ont dÃĐcouvert des chercheurs de l'universitÃĐ de la Colombie-Britannique.
Les scientifiques voulaient vÃĐrifier si la nature de l'explication fournie aux femmes concernant leur inhabiletÃĐ ÂŦstÃĐrÃĐotypiqueÂŧ en mathÃĐmatiques allait avoir un impact sur leur performance rÃĐelle. Il s'agit de la ÂŦmenace du stÃĐrÃĐotypeÂŧ, un concept selon lequel le rappel de croyances associÃĐes depuis longtemps à un groupe incite les membres de ce groupe à se conformer au stÃĐrÃĐotype.
Sur une pÃĐriode de trois ans, les chercheurs de l'universitÃĐ de la Colombie-Britannique ont demandÃĐ Ã 135 femmes de se soumettre à des tests similaires à ceux utilisÃĐs pour l'admission aux ÃĐtudes supÃĐrieures. Chaque femme devait notamment complÃĐter une section mathÃĐmatique complexe, mais seulement aprÃĻs avoir pris connaissance d'un article concernant les diffÃĐrences entre les sexes en mathÃĐmatiques.
Des quatre articles fictifs, le premier faisait valoir qu'il n'existe aucune diffÃĐrence, le second que la diffÃĐrence est d'origine gÃĐnÃĐtique, et le troisiÃĻme que la diffÃĐrence dÃĐcoule de la maniÃĻre dont les mathÃĐmatiques sont enseignÃĐes aux femmes à l'ÃĐcole primaire. Le dernier traitait de la place des femmes dans le monde des arts, puisque les scientifiques croient depuis un moment que le simple fait de rappeler à une femme qu'elle est une femme aura un impact nÃĐgatif sur sa performance.
Les femmes à qui il avait ÃĐtÃĐ expliquÃĐ que leurs expÃĐriences antÃĐrieures ÃĐtaient responsables de leurs habiletÃĐs mathÃĐmatiques ont obtenu deux fois plus de rÃĐponses exactes que les femmes à qui il avait ÃĐtÃĐ expliquÃĐ que leur code gÃĐnÃĐtique ÃĐtait à blÃĒmer. Les femmes à qui on avait rappelÃĐ qu'elles ÃĐtaient des femmes ont aussi moins bien rÃĐussi que celles à qui on avait expliquÃĐ qu'il n'y avait aucune diffÃĐrence.
ÂŦJ'ai ÃĐtÃĐ surpris de l'importance de la rÃĐduction de la menace (du stÃĐrÃĐotype) chez les femmes à qui on avait soulignÃĐ l'importance des expÃĐriences antÃĐrieuresÂŧ, a expliquÃĐ l'auteur de l'ÃĐtude, l'ÃĐtudiant au doctorat Ilan Dar-Nimrod.
La simple mention qu'il puisse exister une diffÃĐrence entre les hommes et les femmes en mathÃĐmatiques peut se rÃĐvÃĐler explosive. L'ÃĐtÃĐ dernier, le prÃĐsident de l'universitÃĐ Harvard, Lawrence Summers, avait ÃĐtÃĐ contraint de dÃĐmissionner aprÃĻs avoir dÃĐclarÃĐ que les femmes sont sous-reprÃĐsentÃĐes dans le domaine des sciences parce qu'elles n'ont pas les capacitÃĐs innÃĐes pour y exceller.
D'autres chercheurs croient que les rÃĐsultats de cette ÃĐtude illustrent bien la complexitÃĐ de l'association entre les gÃĻnes et un comportement donnÃĐ.
Source : Cyberpresse
lu 5937 fois
jeudi 30 novembre 2006
Par Didier MÞller,
jeudi 30 novembre 2006 à 10:01
- Humour/bÊtisier
Je pense que je ne suis pas le seul à avoir vu ce genre de simplification...
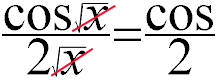
Plus tard dans la journÃĐe, je corrige une ÃĐpreuve et je lis : cos(2x)+sin(2x) = 2x(cos + sin)...
lu 7256 fois
mardi 28 novembre 2006
Par Didier MÞller,
mardi 28 novembre 2006 à 09:04
- Cours en ligne/MOOC
Xmaths est un cours de math en ligne gratuit de Xavier Delahaye.
Il a pour but d'aider les lycÃĐens, les ÃĐtudiants, les personnes prÃĐparant certains concours à voir ou à revoir et à mieux assimiler les diffÃĐrentes notions de mathÃĐmatiques. On y trouve des quiz, des cours, des dÃĐmonstrations à connaÃŪtre et des exercices.
lu 9036 fois
dimanche 26 novembre 2006
Par Didier MÞller,
dimanche 26 novembre 2006 à 09:54
- Sites de mathÃĐmatiques
ABC Maths propose cours, exercices, gÃĐomÃĐtrie dynamique, QCM et animations mathÃĐmatiques de l'ÃĐcole primaire aux classes prÃĐparatoires de lycÃĐe. Les animations, par exemple celles sur les fonctions, sont particuliÃĻrement rÃĐussies. On y trouve aussi un blog d'informations et de divertissements mathÃĐmatiques en images ou sÃĐquences vidÃĐo.
Ne pas confondre avec un autre site homonyme, et qui a presque la mÊme adresse, mais qui est payant.
lu 6738 fois
vendredi 24 novembre 2006
Par Didier MÞller,
vendredi 24 novembre 2006 à 08:06
- Humour/bÊtisier
Monsieur Dehun et Madame EgalzÃĐro ont une fille. Comment l'appellent-ils ?
HÃĐlÃĻne.
Messieurs Exponentiel et Logarithme vont boire un verre. Qui est-ce qui paie ?
Exponentiel, car Logarithme ne paie rien.
P.S. Merci à Quentin pour la seconde blague.
lu 6737 fois
jeudi 23 novembre 2006
Par Didier MÞller,
jeudi 23 novembre 2006 à 12:57
- Sites de mathÃĐmatiques
Le site Studies into Polyhedra - Regular propose de superbes dessins de polyÃĻdres. Tellement superbes qu'ils ÃĐgayeraient une salle de maths...

lu 6003 fois
mercredi 22 novembre 2006
Par Didier MÞller,
mercredi 22 novembre 2006 à 10:46
- Articles/revues
 Lorsque lâon pense aux dÃĐbuts de lâinformatique, viennent à lâesprit dâÃĐnormes ordinateurs dÃĐcorÃĐs dâune multitude de cÃĒbles, meublant des piÃĻces entiÃĻres. Pourtant, derriÃĻre ces mastodontes se cache une machineâĶ de papier. En 1936, alors que les rares machines à calculer dÃĐjà construites peinent à donner le rÃĐsultat pour lequel elles ont ÃĐtÃĐ conçues, un ÃĐtudiant britannique de 24 ans, Alan Turing, imagine une machine dâune simplicitÃĐ enfantine, mais dâune puissance colossale : constituÃĐe dâun ruban, dâune tÊte de lecture et dâune liste dâinstructions, celle-ci rÃĐalise tout ce qui peut Être mis sous la forme dâun algorithme. La multitude des machines devient une : lâordinateur est nÃĐ.
Lorsque lâon pense aux dÃĐbuts de lâinformatique, viennent à lâesprit dâÃĐnormes ordinateurs dÃĐcorÃĐs dâune multitude de cÃĒbles, meublant des piÃĻces entiÃĻres. Pourtant, derriÃĻre ces mastodontes se cache une machineâĶ de papier. En 1936, alors que les rares machines à calculer dÃĐjà construites peinent à donner le rÃĐsultat pour lequel elles ont ÃĐtÃĐ conçues, un ÃĐtudiant britannique de 24 ans, Alan Turing, imagine une machine dâune simplicitÃĐ enfantine, mais dâune puissance colossale : constituÃĐe dâun ruban, dâune tÊte de lecture et dâune liste dâinstructions, celle-ci rÃĐalise tout ce qui peut Être mis sous la forme dâun algorithme. La multitude des machines devient une : lâordinateur est nÃĐ.
Qui est ce jeune homme et comment a-t-il conçu une idÃĐe aussi ingÃĐnieuse ? Telles sont les questions auxquelles Jean LassÃĻgue, chargÃĐ de recherche au CNRS attachÃĐ au Centre de recherche en ÃĐpistÃĐmologie appliquÃĐe de lâÃcole polytechnique, rÃĐpond ici, nous entraÃŪnant sur les traces dâun scientifique qui avait tout pour lui, sauf dâÊtre homosexuel dans une Angleterre conservatrice. Se dessine alors un parcours des plus romanesques : en à peine 20 ans, Turing obtint des rÃĐsultats rÃĐvolutionnaires dans des domaines aussi variÃĐs que les mathÃĐmatiques, la logique, la construction des premiers ordinateurs ou la morphogenÃĻse biologique. Pendant la Seconde Guerre mondiale, au dÃĐpart quasi seul, il dÃĐcoda les messages cryptÃĐs de la marine allemande. Ces gloires ne suffirent pas, toutefois, à racheter, aux yeux de la justice anglaise, son attirance pour les hommes : condamnÃĐ Ã la castration chimique, Turing, à bout de ressources, tira sa rÃĐvÃĐrence dans la fleur de lâÃĒge.
à cÃītÃĐ de ce pÃĻlerinage aux sources de lâinformatique, ce numÃĐro vous propose de dÃĐcouvrir les mathÃĐmatiques indiennes de lâÃĐpoque mÃĐdiÃĐvale, de suivre le parcours de Joseph Norman Lockyer, un pionnier de lâastrophysique qui renouvela la vision des sciences au XIXe siÃĻcle, de rechercher la recette du parfait ÃĐnoncÃĐ de concours, ou encore de goÃŧter au raffinement de lâillustration scientifique du XVIIIe siÃĻcle.
Voir le sommaire.
lu 6395 fois
mardi 21 novembre 2006
Par Didier MÞller,
mardi 21 novembre 2006 à 15:24
- Doc/sÃĐries/films/vidÃĐos
La machine d'AnticythÃĻre est un artefact antique conservÃĐ au MusÃĐe national archÃĐologique d'AthÃĻnes, qu'on pense Être un mÃĐcanisme permettant de calculer la position de certains astres, tels que le soleil et la lune. Elle a ÃĐtÃĐ dÃĐcouverte en 1900 par des pÊcheurs d'ÃĐponges, dans une ÃĐpave prÃĻs des cÃītes de l'ÃŪle grecque d'AnticythÃĻre, entre CythÃĻre et la CrÃĻte. Elle est datÃĐe des alentours de 87 av. J.-C.
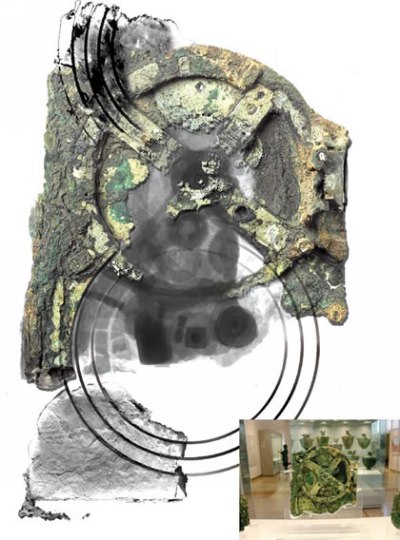
La diversitÃĐ des opinions ne convergent que sur un point : câest un calculateur. Or en Occident, le premier calculateur connu fut celui que crÃĐa Pascal en 1641 (la Pascaline). Soit, pour AnticythÃĻre, une antÃĐrioritÃĐ de 17 siÃĻcles ! Cette machine de bronze, de forme circulaire, actuellement fragmentÃĐe en 3 parties, occupe le volume d'un petit boÃŪtier haut de 21 cm, large de 16 et ÃĐpais de 5 (dimensions dâun livre de taille moyenne). Elle est composÃĐe de 32 ÃĐlÃĐments dont une vingtaine de roues dentÃĐes. Elle devait probablement Être actionnÃĐe à la main ou par un systÃĻme hydraulique. Son fonctionnement se base sur les mouvements diffÃĐrentiels des engrenages permettant de ÂŦ calculer Âŧ la position des astres à un moment donnÃĐ.
Ceci pose immÃĐdiatement nombre de questions, par exemple :
- Comment les Grecs, peu rÃĐputÃĐs pour leur culture technologique, ont-ils pu rÃĐaliser un tel instrument, si en avance sur son temps ?
- Comment une telle technologie a-t-elle pu se crÃĐer puis disparaÃŪtre ?
- Que se serait-il passÃĐ si cette technologie avait pu se rÃĐpandre dans les civilisations grÃĐco-romaine, puis mÃĐdiÃĐvale ?
A voir :
La chaÃŪne PlanÃĻte diffuse ce mois un reportage sur
L'invention de l'ordinateur, oÃđ il est question de la machine d'AnticythÃĻre.
A lire:
lu 8466 fois
lundi 20 novembre 2006
Par Didier MÞller,
lundi 20 novembre 2006 à 10:20
- Enigmes/casse-tÊte
Un cryptarithme est un casse-tÊte purement arithmÃĐtique, oÃđ il s'agit de retrouver une opÃĐration mathÃĐmatique qui a subi une transformation littÃĐrale selon un code bien dÃĐterminÃĐ. Les cryptarithmes les plus courants sont dits de substitution bijective. Voici les rÃĻgles que ces cryptarithmes doivent suivre:
- un chiffre donnÃĐ sera toujours remplacÃĐ par une mÊme lettre;
- une lettre donnÃĐe reprÃĐsente toujours le mÊme chiffre;
- aucun nombre ne peut commencer par un zÃĐro;
- les accents sont sans incidence (sauf prÃĐcision de l'auteur);
- idÃĐalement, il n'y a qu'une solution.
Ãvidemment, les plus beaux cryptarithmes sont ceux dont les lettres forment des mots du dictionnaire. Si en plus ces mots ont un rapport entre eux, cela confine à l'art. Par exemple :
CINQ
+ CINQ
+VINGT
------
TRENTE
Pour en construire, il existe un site gÃĐnial:
Cryptarithmetic Puzzle Solver. Essayez!
A voir aussi :
lu 6777 fois
< 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 >

 Parmi tous les tours de magie, il existe un ensemble particulier, celui des "tours de cartes automatiques". Pouvant Être faits avec un jeu de carte usuel et ne demandant aucune manipulation prÃĐparatoire des cartes, ils sont liÃĐs aux mathÃĐmatiques par des outils simples (symÃĐtrie, comptage, permutations...).
Parmi tous les tours de magie, il existe un ensemble particulier, celui des "tours de cartes automatiques". Pouvant Être faits avec un jeu de carte usuel et ne demandant aucune manipulation prÃĐparatoire des cartes, ils sont liÃĐs aux mathÃĐmatiques par des outils simples (symÃĐtrie, comptage, permutations...).



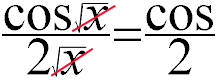

 Lorsque lâon pense aux dÃĐbuts de lâinformatique, viennent à lâesprit dâÃĐnormes ordinateurs dÃĐcorÃĐs dâune multitude de cÃĒbles, meublant des piÃĻces entiÃĻres. Pourtant, derriÃĻre ces mastodontes se cache une machineâĶ de papier. En 1936, alors que les rares machines à calculer dÃĐjà construites peinent à donner le rÃĐsultat pour lequel elles ont ÃĐtÃĐ conçues, un ÃĐtudiant britannique de 24 ans, Alan Turing, imagine une machine dâune simplicitÃĐ enfantine, mais dâune puissance colossale : constituÃĐe dâun ruban, dâune tÊte de lecture et dâune liste dâinstructions, celle-ci rÃĐalise tout ce qui peut Être mis sous la forme dâun algorithme. La multitude des machines devient une : lâordinateur est nÃĐ.
Lorsque lâon pense aux dÃĐbuts de lâinformatique, viennent à lâesprit dâÃĐnormes ordinateurs dÃĐcorÃĐs dâune multitude de cÃĒbles, meublant des piÃĻces entiÃĻres. Pourtant, derriÃĻre ces mastodontes se cache une machineâĶ de papier. En 1936, alors que les rares machines à calculer dÃĐjà construites peinent à donner le rÃĐsultat pour lequel elles ont ÃĐtÃĐ conçues, un ÃĐtudiant britannique de 24 ans, Alan Turing, imagine une machine dâune simplicitÃĐ enfantine, mais dâune puissance colossale : constituÃĐe dâun ruban, dâune tÊte de lecture et dâune liste dâinstructions, celle-ci rÃĐalise tout ce qui peut Être mis sous la forme dâun algorithme. La multitude des machines devient une : lâordinateur est nÃĐ. 