L'intégrité

• Accueil
• Cryptographie
• Stéganographie
• Cryptanalyse
• Lexique

Un des problèmes annexes à la cryptographie est la vérification de l'intégrité d'un message: comment savoir si le message que l'on reçoit n'a pas été modifié en cours de route? Ce problème peut aussi se poser avec Internet: comment savoir si la version du logiciel X mis en téléchargement sur le web est bien le logiciel original et non pas une version avec un virus? Quand la police confisque un disque dur pour une enquête, a aussi besoin d'assurer l'intégrité de ce disque pour prouver que son contenu n'a pas été modifié entre la confisquation et l'éventuel procès.

La réponse à ces problèmes est la notion de fonction de hachage à sens unique. Cette fonction (H), qui doit être rapide à calculer, transforme un message M de longueur arbitraire en une empreinte numérique h de taille fixée:

Cette fonction doit en outre avoir les propriétés suivantes:

• étant donné un message M, il est facile de calculer l'empreinte h,
• étant donné une empreinte h, il est difficile de calculer le message M,
• résistance forte à la collision: il est difficile de trouver deux messages M et M' tels que H(M)=H(M').

Alice envoie à Bob le message lui-même et son empreinte qu'elle aura calculée. Bob calcule à son tour l'empreinte du message puis la compare avec celle qu'il a reçue. Si ce sont les mêmes, le message n'a pas été modifié.
On peut voir une analogie avec les empreintes digitales: c'est aussi une manière fiable de vérifier l'identité d'un individu avec une petite quantité d'informations.

Deux exemples de fonction de hachage

MD4 et MD5

SHA-1

Le programme javascript ci-dessous va illustrer comment une petite modification d'un texte change complètement son empreinte. Après avoir calculé les empreintes du texte donné en exemple, remplacez le "é" par un "e" du texte clair pour voir la différence.

	Texte	Empreinte numérique
	Empreinte MD4
	Empreinte MD5
	Empreinte SHA-1

L'un des exemples les plus étranges dans l'histoire des mathématiques de ce que l'on pourrait appeler une empreinte d'un document semble être dû à Newton. Entre 1673 et 1676 a commencé ce que Maor appelle la grande controverse entre Newton et Leibniz au sujet de la primauté de l'invention du calcul différentiel. Leibniz essayait de savoir ce que Newton savait. Ils ont échangé quelques courriers mais Newton, obsédé par l'idée qu'on puisse s'approprier une de ses découvertes, n'a finalement donné que peu d'informations à Leibniz. L'un des derniers messages de Newton, a priori très énigmatique, est le suivant:

Il s'agit en fait d'une sorte d'empreinte du message suivant:

On peut vérifier que ce message contient bien six fois le caractère "a", deux fois le caractère "c", etc. (u et v sont confondus).

Attaque des anniversaires

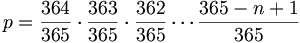
Or, cette probabilité tombe en dessous de 0.5 quand n=23.

Ce «paradoxe» a son importance en cryptographie, lorsqu'on étudie les fonctions de hachage. Pour que cette fonction soit fiable, il ne faut pas que l'on puisse produire deux textes aux sens très différents mais donnant la même empreinte.
Si l'empreinte est codée sur b bits, il y a 2^b empreintes possibles. Si l'on prend k textes différents, la probabilité pour que deux textes aient la même empreinte est donc:

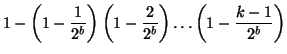
Combien l'attaquant doit-il essayer de textes avant de trouver la même empreinte avec une probabilité d'au moins 0.5? Le tableau suivant donne des valeurs pour différentes valeurs de b:

On voit sur ce tableau qu'on a environ une chance sur deux de trouver deux textes à l'empreinte identique en en essayant un nombre de l'ordre de la racine carrée du nombre d'empreintes. On considère en général que, pour obtenir un niveau de sécurité correct, il faut prendre une taille d'empreinte d'au moins 128 bits.

Références

• Schneier Bruce, Cryptographie appliquée, International Thomson Publishing France, Paris, 1997, pp. 460-464
• Stinson Douglas, Cryptographie - Théorie et pratique, Vuibert Informatique, Paris, 2001, chapitre 7
• FIPS PUB 180-2

• Le paradoxe des anniversaires

Didier Müller, 27.1.21