Le cryptosystème RSA

L'implémentation fut achevée en 1978 par Rivest, Shamir et Adleman. Depuis, ce système de chiffrement est appelé RSA, qui sont les initiales de ces trois chercheurs.

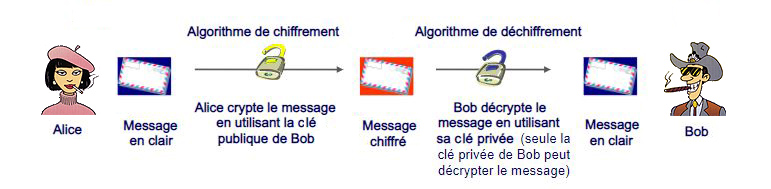
Fonctionnement du cryptosystème RSA

On appellera Bob la personne qui désire recevoir un message chiffré, et Alice la personne qui envoie le message.

1. Choix de la clef



Bob choisit deux grands entiers naturels premiers p et q (d'environ 100 chiffres chacun ou plus) et fait leur produit n = p·q. Puis il choisit un entier e premier avec (p-1)·(q-1). Enfin, il publie dans un annuaire, par exemple sur le web, sa clef publique: (RSA, n, e).

 

2. Chiffrement

Alice veut donc envoyer un message à Bob. Elle cherche dans l'annuaire la clef de chiffrement qu'il a publiée. Elle sait maintenant qu'elle doit utiliser le système RSA avec les deux entiers n et e (prenons par exemple n=5141=53·97 et e=7, premier avec 52·96=4992). Elle transforme en nombres son message en remplaçant par exemple chaque lettre par son rang dans l'alphabet.

"JEVOUSAIME" devient : "10 05 22 15 21 19 01 09 13 05".

Puis elle découpe son message chiffré en blocs de même longueur représentant chacun un nombre plus petit que n. Cette opération est essentielle, car si on ne faisait pas des blocs assez longs (par exemple si on laissait des blocs de 2 dans notre exemple), on retomberait sur un simple chiffre de substitution que l'on pourrait attaquer par l'analyse des fréquences.

Son message devient : "010 052 215 211 901 091 305"

Un bloc B est chiffré par la formule C = Be mod n, où C est un bloc du message chiffré qu'Alice enverra à Bob.

Après avoir chiffré chaque bloc, le message chiffré s'écrit : "0755 1324 2823 3550 3763 2237 2052".

3. Déchiffrement

Bob calcule à partir de p et q, qu'il a gardés secrets, la clef d de déchiffrage (c'est sa clef privée). Celle-ci doit satisfaire l'équation e·d mod ((p-1)(q-1)) = 1. Ici, d=4279.
Chacun des blocs C du message chiffré sera déchiffré par la formule B = Cd mod n.

Il retrouve : "010 052 215 211 901 091 305"

L'instruction d=PowerMod[e,-1,(p-1)(q-1)] de Wolfram Alpha permet de calculer d facilement. On peut aussi utiliser l'algorithme d'Euclide étendu pour calculer d = e-1 mod (p-1)(q-1).

En regroupant les chiffres deux par deux et en remplaçant les nombres ainsi obtenus par les lettres correspondantes, Il sait enfin qu'Alice l'aime secrètement, sans que personne d'autre ne puisse le savoir.

 

Intérêt de la méthode

Tout l'intérêt du système RSA repose sur le fait qu'à l'heure actuelle il est pratiquement impossible de retrouver dans un temps raisonnable p et q à partir de n si celui-ci est très grand (ou alors, si c'est possible, les cryptanalystes qui ont trouvé la méthode la gardent secrète). Bob est donc le seulà pouvoir calculer d dans un temps court. De plus, il n'a jamais à transmettre les entiers p et q, ce qui empêche leur piratage.

Programme Javascript

Utilisation: La personne voulant déchiffrer le message doit posséder toutes les clefs, alors que les autres ne connaissent que les clefs publiques. Ici, les clefs personnelles sont p, q, d, les clefs publiques sont e et n. Le paramètre "Taille des blocs" indique comment regrouper les chiffres avant le chiffrement proprement dit. Avant de commencer, il faut choisir entre la table de conversion simple (les caractères à utiliser se limiteront alors aux majuscules et à l'espace) et la table de conversion étendue (qui permet les accents, les minuscules, les chiffres et d'autres caractères spéciaux). Vous pouvez utiliser d'autres tables de conversion, mais toutes les tables doivent contenir le symbole " " (espace).

Pour chiffrer: Il suffit d'entrer e, n et la taille des blocs (c'est la clef publique donnée par la personne qui déchiffrera) ainsi que le message dans le champ "Message clair". Appuyez ensuite sur "Chiffrer".

Pour déchiffrer: Entrez, en plus de e, n et la taille des blocs, la valeur de d (ou simplement entrez les trois nombres originaux de p, q et e puis appuyez sur le bouton calcul). Placez le cryptogramme dans le champ "Message chiffré", puis appuyez sur "Déchiffrer".

Création des clefs de (dé)chiffrement: Entrez des nombres premiers dans les champs p et q, puis e satisfaisant la condition énoncée dans la première partie de la page. Il faut que les 3 nombres soient différents. Appuyez ensuite sur le bouton "Calcul" pour trouver n et d. Plus les nombres sont grands, plus de décryptement sera difficile, mais le temps de déchiffrement augmentera aussi.

Clef privée p : q : e : Taille des blocs :
Clef publique n = p·q : d :
     
Table de conversion
Message clair
Message chiffré

Exercices

Chiffrement / déchiffrement

  1. Créez votre clef privée et votre clef publique (blocs de 3 pour tout le monde).
  2. Une fois que c'est fait, publiez votre clef publique en l'écrivant au tableau noir.
  3. Ecrivez à la personne de votre choix un message chiffré en utilisant sa clef publique que vous aurez repérée au tableau noir (utilisez la table de conversion étendue).
  4. Déchiffrez le message que vous avez reçu.

Décryptement

Bob a comme clef publique (RSA, 57418111, 41). Alice lui a envoyé le message suivant (en utilisant la table de conversion étendue ci-dessus avec des blocs de longueur 3) :

49512134 21375717 37445940 22747071 08018685 50261082 26773363 27745904 13885242 12693777 35737968 21484174 49353519 52913189 43691901 22649799
51337833 34008132 18071650 31968614 44063246 41571582 43691901 06985600 34646750 31968614 34211732 21872035 43691901 53962589 26422724 25603725
08056422 47444427 36818942 27745904 04901538 10222409 47571156 48818768 35737968 36726070 43691901 28649787

Décryptez ce message.

Programmation

Ecrivez un programme Python qui chiffre et déchiffre un texte en utilisant le cryptosystème RSA. Codez les caractères avec le code ASCII et faites des blocs de 4. Solution

Vidéos

Références

  Didier Müller, 17.3.25