Les courbes elliptiques

Les spécialistes en cryptographie font de plus en plus appel à une technique qui s'appuie sur des courbes elliptiques, proposée indépendamment par Victor Miller et Neal Koblitz en 1985. La théorie des courbes elliptiques en général est un domaine riche et a donné de nombreux résultats, dont la preuve du dernier théorème de Fermat par Andrew Wiles.
Une courbe elliptique est un objet très simple mais qui a des propriétés tout à fait surprenantes. Elles ont normalement la forme suivante:

y2+a1xy+a3y=x3+a2x2+a4x+a6

Pour leur usage en cryptographie, a1, a2 et a3 doivent être égaux à 0. Comme les cryptographes ont l'habitude de renommer a4=a et a6=b, on obtient

y2=x3+ax+b

Un exemple typique de courbe elliptique est donné sur la figure ci-dessous. Son équation est y2=x3-5x2+3.

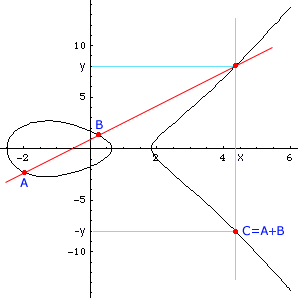
Addition de deux points

Prenons deux points A et B sur cette courbe. En général, la courbe passant par A et B recoupe la courbe en un troisième point de coordonnées (x, y). Son symétrique (x, -y) est lui aussi sur la courbe et on le désigne par A+B pour signifier qu'il est construit à l'aide de A et B. La chose surprenante est que cette opération "+" possède toutes les propriétés de l'addition des nombres. C'est-à-dire que l'on peut faire tous les calculs de type addition, soustraction et division avec un reste entier que nous faisons sur la droite des nombres réels sur cet objet tordu que constitue une courbe elliptique.
Il est possible, comme l'ont démontré Miller et Koblitz, de coder avec cette opération bizarre au lieu de travailler avec l'addition usuelle. Il en résulte une plus grande complexité des calculs qui fait dire aux spécialistes que le chiffrement par la méthode des courbes elliptiques avec une clef de 192 bits assure le même niveau de sécurité qu'une clef de 1024 bits pour la méthode RSA. Il est donc probable que cette méthode sera de plus en plus utilisée pour transmettre les clefs.

Règles de l'addition
Soit la courbe elliptique cryptographique y2 mod p = (x3 + ax + b) mod p. On reconnaît l'équation déjà vue ci-dessus, sauf que l'on travaille modulo p. Le nombre p doit être un nombre premier.
Lors des calculs, il arrive parfois que l'on doive faire une division par 0. Quand cela arrive, le point résultat sera appelé "infini".
  1. infini + infini = infini
  2. (x1,y1) + infini = (x1,y1)
  3. (x1,y1) + (x1,-y1) = infini
  4. Si x1 x2, (x1,y1) + (x2,y2) = (x3,y3), avec
        x3 = (k2-x1-x2) mod p
        y3 = (k(x1-x3)-y1) mod p
        où k = (y2-y1) · (x2-x1)-1 mod p
  5. Si y1 0, (x1,y1) + (x1,y1) = 2(x1,y1) = (x3,y3), avec
        x3 = (k2-2x1) mod p
        y3 = (k(x1-x3)-y1) mod p
        où k = (3x12+a) · (2y1)-1 mod p

On remarque que pour calculer k, on doit trouver l'inverse d'un nombre modulo p. Pour trouver cet inverse, on utilise l'algorithme d'Euclide étendu.

Multiplication d'un point par un nombre entier

On remplace la multiplication par une série d'additions. Prenons un exemple. Soit la courbe y2 mod 11 = (x3 + x + 2) mod 11.
Calculons d·P, avec d=3 et P=(4, 2). On peut vérifier que le point P appartient bien à la courbe elliptique.
On peut remplacer 3·P par P + P + P. Calculons d'abord P + P.
D'après la règle 5, P + P = (4, 2) + (4, 2) = (8, 4) = 2·P.
D'après la règle 4, 2·P + P = (8, 4) + (4, 2) = (2, 10) = 3·P.

Exercice : vérifiez les calculs de 2·P et 3·P! Ces points appartiennent-ils à la courbe elliptique donnée?

Échange de clefs

Alice et Bob se mettent d'accord (publiquement) sur une courbe elliptique E(a,b,p), c'est-à-dire qu'ils choisissent une courbe elliptique y2 mod p = (x3+ax2+b) mod p. Ils se mettent aussi d'accord, publiquement, sur un point P situé sur la courbe.

Secrètement, Alice choisit un entier dA, et Bob un entier dB. Alice envoie à Bob le point dAP, et Bob envoie à Alice dBP. Chacun de leur côté, ils sont capables de calculer dA(dBP)=dB(dAP)=(dAdB)P, qui est un point de la courbe, et constitue leur clef secrète commune.

Sécurité
Si Eve a espionné leurs échanges, elle connaît E(a,b,p), P, dAP et dBP. Pour pouvoir calculer dAdBP, il faut pouvoir calculer dA connaissant P et dAP. C'est ce que l'on appelle résoudre le logarithme discret sur une courbe elliptique. Or, actuellement, si les nombres sont suffisamment grands, on ne connaît pas de méthode efficace pour résoudre ce problème en un temps raisonnable.

Inconvénients

Références

  Didier Müller, 27.1.21