Les registres à décalage à rétroaction linéaire (LFSR)

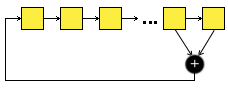
Cette méthode pour générer des nombres pseudo-aléatoires est basée sur les registres à décalage à rétroaction linéaire (Linear Feedback Shift Register en anglais). L'idée est de commencer avec un registre rempli arbitrairement avec des 0 et des 1, puis de décaler cette suite d'un cran vers la droite. On remplira la position tout à gauche par la somme (modulo 2) du contenu des deux registres les plus à droite (avant le décalage), comme l'indique le schéma ci-dessous, où chaque carré jaune représente un bit et le rond noir l'addition modulo 2:

Remarque: on peut imaginer d'autres façons de remplir la position tout à gauche, par exemple, en additionnant modulo 2 les trois derniers bits, ou le dernier et l'antépénultième, etc.

Exemple

Prenons un registre à 4 bits que l'on remplira pour commencer avec le motif 1111. En utilisant le schéma ci-dessus on obtiendra successivement:

En convertissant les contenus successifs du registre en base 10, on obtient une suite pseudo-aléatoire. Évidemment, le processus cycle quand on retrouve le motif initial.
Remarquons que l'on a obtenu tous les motifs possibles, sauf 0000, et que cela aurait été le cas pour tous les états initiaux possibles, sauf 0000. On a trouvé dans notre exemple un cycle de longueur maximale.
En général, pour un registre à n bits, il est possible d'arranger les choses pour que la longueur du cycle soit 2ⁿ-1. Ainsi, pour n grand, on obtient de bons générateurs de nombres pseudo-aléatoires. Typiquement, on peut utiliser n=31 ou n=63. Comme pour les générateurs congruentiels linéaires, les propriétés mathématiques de ces registres ont été beaucoup étudiées. Par exemple, on sait beaucoup de choses sur sur le choix des positions à utiliser pour la rétroaction pour obtenir un cycle de longueur maximale. Ainsi, pour n=31, on peut faire la rétroaction avec la position 0 et au choix les positions 4, 7, 8, 14, 19, 25, 26 ou 29 (les positions sont numérotées de droite à gauche en commençant par 0).

Exercice

Programmez en Mathematica un générateur de nombres pseudo-aléatoires basé sur un registre à décalage de n bits. Ajoutez à votre programme une fonction permettant de calculer la longueur d'un cycle. Pour n=7, testez avec votre programme les 21 couples de positions possibles pour effectuer la rétroaction. On supposera que le motif initial du registre est 1,1,1,1,1,1,1.

Fonctions Mathematica utiles: AppendTo, Delete, For, FromDigits, KSubsets, If, Length, Mod, Module, Prepend, Print, N, While.
Fichier d'extension: DiscreteMath`Combinatorica`

Références

• Robert Sedgewick, Algorithms, Addison-Wesley, 2ème édition, 1988, pp. 514-516
• Linear Feedback Shift Registers
• Pseudo-Random Number Generation Routine for the MAX765x Microprocessor

Didier Müller, 23.1.03