Décryptement automatique d'un chiffre de Vigenère

On essaie plusieurs longueurs de clef (1, 2, 3, ..., 20), jusqu'à ce qu'on trouve un indice de coïncidence supérieur à un "indice-plancher" de 0.06 (voir le test de Friedman). On suppose que c'est la longueur de notre clef.
Remarque: si la clef est de longueur 1, on a affaire à un chiffre de César.

Deuxième étape: trouver la clef

Il faut bien se rappeler que chaque lettre de la clef donne en fait le décalage d'un chiffre de César ("A" = pas de décalage, "B" = décalage de 1, ..., "Z" = décalage de 25). On cherche donc la clef lettre par lettre en essayant les 26 décalages possibles.
Pour trouver le bon décalage, on s'y prend de la même façon que pour le décryptement manuel: on compare l'histogramme théorique avec l'histogramme des lettres du cryptogramme. Pour trouver la première lettre de la clef, on prendra les lettres de rangs 1, 1+longueur_clef, 1+2·longueur_clef, ...); pour trouver la deuxième lettre de la clef, on prendra les lettres de rangs 2, 2+longueur_clef, 2+2·longueur_clef, ...); etc.


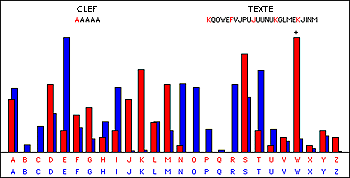
Situation initiale	Après le décalage qui minimise les écarts entre les bâtons des histogrammes bleu (théorique) et rouge.

Pour chacun des 26 bâtons, on calcule la différence de hauteur (en valeur absolue) entre le bâton bleu et le bâton rouge qui lui est superposé. On cumule ensuite les 26 écarts obtenus, ce qui nous donne l'écart cumulé pour le premier décalage.
On décale ensuite l'histogramme rouge d'un cran et on refait le même calcul. On procède ainsi pour chacun des 26 décalages.
Le décalage le plus probable est celui qui minimise l'écart cumulé. Visuellement, cela revient à "caler au mieux" l'histogramme rouge sur le bleu. Ce décalage nous donne une lettre de la clef (dans l'exemple ci-dessus, la première lettre de la clef est S).
En procédant ainsi pour toutes les lettres de la clef, on finira par trouver le mot utilisé pour chiffrer le message.

Programme javascript de décryptement

Le décryptement n'est pas fiable à 100%, surtout si le cryptogramme est court. Aussi est-il possible, dans le programme javascript ci-dessous, de modifier manuellement la clef et de refaire une tentative de décryptement (bouton "Essayer une autre clef"). Il est aussi possible de modifier l'indice-plancher.

Programmation

Ecrivez un programme Python qui décrypte automatiquement un message chiffré avec Vigenère. Solution.