Le décryptement d'un message chiffré avec le chiffre de Collon se fait en deux phases:
Il faut pour cela essayer systématiquement les longueurs les
unes après les autres (généralement il suffit d'essayer les longueurs entre
1 et 15). Pour chaque longueur, on observe les fréquences des bigrammes. Si
leur histogramme correspond plus ou moins à l'histogramme
des fréquences des lettres dans la langue choisie, il est très probable
que la longueur des séries correspondantes soit la bonne. On écrit alors la
suite des bigrammes obtenus.
On peut aussi observer qu'au maximum 25 bigrammes différents
peuvent apparaître. S'il y en a plus, ce n'est pas la bonne longueur des séries.
![]() Ce programme Python vous aidera dans cette recherche.
Ce programme Python vous aidera dans cette recherche.
Une fois la longueur des séries déterminée, on a affaire à une substitution simple. On peut donc utiliser la méthode de l'analyse des fréquences pour décrypter les bigrammes. On peut aussi tenter la méthode du mot probable.
Soit le cryptogramme suivant, sachant de plus que le message clair contient "Gérard de Nerval":
FCNCX ZXZNR CRUVZ XNNCC ZVXYU RNCYU ZVNRC UVZXV CNCCX UZZNC CRUUV XNNCR UZZUC RRCZV VZRUN RXUXX URCFU VXZCN NCXXX ZRFNC XZZXC RRCZU ZZCCF FYXZZ CFCUZ UZUUR RCXYU XFFRN ZZXUN RNNZX ZVNFR NUUUV NNCNU ZXUNN RCVUZ ZRCRC ZZVUF RRNZX UZCRR NZVZV RCCNU XZUNR UUZXU XRRCR UXXVC NRNXU VUNCR RVXUV CCFCY ZZZRR UCVXV ZCFNR UZVUR CNRZZ ZXNRC RZUZV RCFCV ZVZRR RRUXU ZRCNC ZZUZR URFUV XZCUR NYYUZ CNVV
Si la longueur des séries utilisée était de 1, nous aurions 39 bigrammes, ce qui est impossible. On obtiendrait en effet:
FC NC XZ XZ NR CR UV ZX NN CC ZV XY UR NC YU ZV NR CU VZ XV CN CC XU ZZ NC CR UU VX NN CR UZ ZU CR RC ZV VZ RU NR XU XX UR CF UV XZ CN NC XX XZ RF NC XZ ZX CR RC ZU ZZ CC FF YX ZZ CF CU ZU ZU UR RC XY UX FF RN ZZ XU NR NN ZX ZV NF RN UU UV NN CN UZ XU NN RC VU ZZ RC RC ZZ VU FR RN ZX UZ CR RN ZV ZV RC CN UX ZU NR UU ZX UX RR CR UX XV CN RN XU VU NC RR VX UV CC FC YZ ZZ RR UC VX VZ CF NR UZ VU RC NR ZZ ZX NR CR ZU ZV RC FC VZ VZ RR RR UX UZ RC NC ZZ UZ RU RF UV XZ CU RN YY UZ CN VV
Si la longueur des séries utilisée était de 2, nous aurions 42 bigrammes, ce qui est impossible. On obtiendrait alors:
FN CC XX ZZ NC RR UZ VX NC NC ZX VY UN RC YZ UV NC RU VX ZV CC NC XZ UZ NC CR UV UX NC NR UZ ZU CR RC ZV VZ RN UR XX UX UC RF UX VZ CN NC XX XZ RN FC XZ ZX CR RC ZZ UZ CF CF YZ XZ CC FU ZZ UU UR RC XU YX FR FN ZX ZU NN RN ZZ XV NR FN UU UV NC NN UX ZU NR NC VZ UZ RR CC ZV ZU FR RN ZU XZ CR RN ZZ VV RC CN UZ XU NU RU ZU XX RC RR UX XV CR NN XV UU NR CR VU XV CF CC YZ ZZ RU RC VV XZ CN FR UV ZU RN CR ZZ ZX NC RR ZZ UV RF CC VV ZZ RR RR UU XZ RN CC ZU ZZ RR UF UX VZ CR UN YU YZ CV NV
Si la longueur des séries utilisée était de 3, nous aurions 57 bigrammes, ce qui est impossible. On obtiendrait:
FC CX NZ XR ZC NR UX VN ZN CV CX ZY UC RY NU ZR VC NU VV ZC XN CU CZ XZ NR CU CU VN XC NR UU ZC ZR RV CV ZZ RR UX NU XR XC UF UZ VC XN NX CX XZ RC FX NZ ZR XR CC ZZ UC ZC FX FZ YZ CU FZ CU ZR UR UC XX YF UF RZ NX ZU NN RZ NX ZF VR NN UV UN UN CZ NX UU NC NV RU ZC ZR RC ZU ZF VR RX NU ZZ CN RZ RV ZC VC RN UU XN ZR UX UU ZX RR RU CX XN VR CN XU UN VC RX RU VV CC CY FZ ZR ZU RC VZ XC VF NZ RV UU RR CZ NZ ZR XC NR ZV UR ZC FZ CV VZ RR RU RX UC ZN RC ZZ ZR UU RV FX UZ CN UY RY UN ZV CV
Par contre, si la longueur des séries utilisée est de 4, nous avons 22 bigrammes, ce qui est possible. L'histogramme des fréquences des bigrammes est alors le suivant:
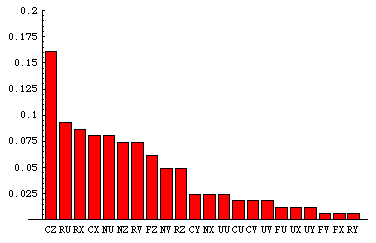
et le cryptogramme "démêlé" est :
FX CZ NX CZ NU RV CZ RX NZ NV CX CY UY RU NZ CV NV RZ CX UV CX NU CZ CZ NU CU CV RX NU NZ CZ RU CZ RV RV CZ RX UU NX RX UU RV CX FZ CX NX NX CZ RX FZ NZ CX CZ RU RZ CZ CY CX FZ FZ CZ FU CZ UU UX RY RU CX FZ FZ RX NU NZ RX NZ NV NU FU RU NV NU NZ CX NU NV NU RZ CZ RZ CZ RV CU FZ RX RU NZ CZ RV RZ NV RU CX CZ NU NZ RX UU UX RU RX CX RV CX NU RV NU NV CX RU RV CY CZ FZ CZ RV RX UV CZ CU FZ NV RU RZ CZ NZ RX NZ RU CZ RV RV CZ FV CZ RU RX RU RZ RZ CZ NU CZ RU UV RX FZ CY UY RU NZ CV NV "
Nous pouvons maintenant attaquer ce cryptogramme à l'aide de l'analyse des fréquences.
Après avoir remplacé "CZ" (le bigramme le plus fréquent) par "e", on obtient:
"FX e NX e NU RV e RX NZ NV CX CY UY RU NZ CV NV RZ CX UV CX NU e e NU CU CV RX NU NZ e RU e RV RV e RX UU NX RX UU RV CX FZ CX NX NX e RX FZ NZ CX e RU RZ e CY CX FZ FZ e FU e UU UX RY RU CX FZ FZ RX NU NZ RX NZ NV NU FU RU NV NU NZ CX NU NV NU RZ e RZ e RV CU FZ RX RU NZ e RV RZ NV RU CX e NU NZ RX UU UX RU RX CX RV CX NU RV NU NV CX RU RV CY e FZ e RV RX UV e CU FZ NV RU RZ e NZ RX NZ RU e RV RV e FV e RU RX RU RZ RZ e NU e RU UV RX FZ CY UY RU NZ CV NV"
Utilisons maintenant le mot connu. On a mis en bleu la séquence correspondant à Gérard de Nerval. On trouve immédiatement les correspondances:
| a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | x | y | z |
| RX | RZ | CZ | FV | FZ | NU | RU | UV |
On obtient après remplacement:
FX e NX e n RV e a NZ NV CX CY UY r NZ CV NV d CX v CX n e e n CU CV a n NZ e r e RV RV e a UU NX a UU RV CX l CX NX NX e a l NZ CX e r d e CY CX l l e FU e UU UX RY r CX l l a n NZ a NZ NV n FU r NV n NZ CX n NV n d e d e RV CU l a r NZ e RV d NV r CX e n NZ a UU UX r a CX RV CX n RV n NV CX r RV CY e l e RV a v e CU l NV r d e NZ a NZ r e RV RV e g e r a r d d e n e r v a l CY UY r NZ CV NV "
On remarque deux structures similiaires (en bleu) où l'on peut deviner les mots "enchanteresse" et "ta tresse". On peut donc essayer les correspondances:
| a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | x | y | z |
| RX | CU | RZ | CZ | FV | CV | FZ | NU | RU | RV | NZ | UV |
On obtient alors:
FX e NX e n s e a t NV CX CY UY r t h NV d CX v CX n e e n c h a n t e r e s s e a UU NX a UU s CX l CX NX NX e a l t CX e r d e CY CX l l e FU e UU UX RY r CX l l a n t a t NV n FU r NV n t CX n NV n d e d e s c l a r t e s d NV r CX e n t a UU UX r a CX s CX n s n NV CX r s CY e l e s a v e c l NV r d e t a t r e s s e g e r a r d d e n e r v a l CY UY r t h NV
On peut maintenant deviner les mots "divine" (en bleu), "aux" (en vert), et "l'or" (en rouge), ce qui nous donne les voyelles "i", "o", "u" et la consonne "x".
| a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | x | y | z |
| RX | CU | RZ | CZ | FV | CV | CX | FZ | NU | NV | RU | RV | NZ | UU | UV | UX |
FX e NX e n s e a t o i CY UY r t h o d i v i n e e n c h a n t e r e s s e a u NX a u s i l i NX NX e a l t i e r d e CY i l l e FU e u x RY r i l l a n t a t o n FU r o n t i n o n d e d e s c l a r t e s d o r i e n t a u x r a i s i n s n o i r s CY e l e s a v e c l o r d e t a t r e s s e g e r a r d d e n e r v a l CY UY r t h o"
Les dernières correspondances se trouvent aisément:
| a | b | c | d | e | f | g | h | i | j | k | l | m | n | o | p | q | r | s | t | u | v | x | y | z |
| RX | RY | CU | RZ | CZ | FU | FV | CV | CX | FX | FZ | CY | NU | NV | NX | RU | RV | NZ | UU | UV | UX | UY |
On obtient enfin:
je pense a toi myrtho divine enchanteresse au pausilippe altier de mille feux brillant a ton front inonde des clartes d orient aux raisins noirs meles avec l or de ta tresse gerard de nerval myrtho"
On peut si l'on veut s'amuser à reconstituer la grille de chiffrement. La première colonne est constituée des premières lettres des bigrammes (C, F, N, R, U), la dernière ligne par les deuxièmes lettres (U, V, X, Y et Z). La lettre claire correspondant au bigramme constitué de deux lettres identiques est située dans la case en bas à gauche de la grille (ici le U). On peut ensuite facilement placer les autres lettres dans la grille grâce au dernier tableau de correspondances obtenus. Moyennant quelques permutations de lignes, on peut même retrouver le mot de passe.
|
|
|
|
|
Le mot de passe était "chimères".