mardi 27 juin 2023
The Korean king's magic square: a brilliant algorithm in a k-drama (plus geomagic squares) - Mathologer
Par Didier MÞller, mardi 27 juin 2023 à 08:32 - Doc/sÃĐries/films/vidÃĐos
lu 918 fois
Ce blog a pour sujet les mathématiques et leur enseignement
au Lycée. Son but est triple.
Premièrement, ce blog est pour moi une manière idéale de
classer les informations que je glâne au cours de mes voyages en Cybérie.
Deuxièmement, ces billets me semblent bien adaptés à la
génération zapping de nos élèves. Ces textes courts
et ces vidéos, privilégiant le côté ludique des maths,
pourront, je l'espère, les intéresser et leur donner l'envie d'en
savoir plus.
Enfin, c'est un bon moyen de communiquer avec des collègues de toute
la francophonie.
mardi 27 juin 2023
Par Didier MÞller, mardi 27 juin 2023 à 08:32 - Doc/sÃĐries/films/vidÃĐos
lu 918 fois
vendredi 23 juin 2023
Par Didier MÞller, vendredi 23 juin 2023 à 23:14 - Doc/sÃĐries/films/vidÃĐos
lu 1050 fois
jeudi 22 juin 2023
Par Didier MÞller, jeudi 22 juin 2023 à 06:20 - Voyages au pays des maths
lu 964 fois
mercredi 21 juin 2023
Par Didier MÞller, mercredi 21 juin 2023 à 06:58 - Illusions
Les images et les gifs dans le lien ci-dessous sont si trompeurs qu'on a l'impression que c'est de la magie. Mais pour ÃĐviter de trop vous enfumer le cerveau, on a ajoutÃĐ la solution pour certaines illusions d'optique. Le rÃĐsultat n'en reste pas moins fascinant.
Lire l'article de Sergio Minnig sur Watson
lu 908 fois
mardi 20 juin 2023
Par Didier MÞller, mardi 20 juin 2023 à 08:35 - Voyages au pays des maths
lu 1101 fois
lundi 19 juin 2023
Par Didier MÞller, lundi 19 juin 2023 à 11:32 - Voyages au pays des maths
lu 1090 fois
dimanche 18 juin 2023
Par Didier MÞller, dimanche 18 juin 2023 à 06:11 - Livres/e-books

Il ÃĐtait une fois le zÃĐro
Antoine Houlou-Garcia
Alisio (13 juin 2023)
208 pages
PrÃĐsentation de l'ÃĐditeur
Difficile dâimaginer les mathÃĐmatiques sans lui, et pourtant le zÃĐro a brillÃĐ par son absence pendant des milliers dâannÃĐes. On le pensait absurde, voire dangereux.
Point de dÃĐpart, prÃĐsence dâune absence, incarnation du vide, porte ouverte sur lâinfini, le zÃĐro est une rÃĐvolution. Il a transformÃĐ la maniÃĻre de calculer et permis lâÃĐmergence de lâalgÃĻbre, du calcul infinitÃĐsimal â et de lâinformatique. à travers dâextraordinaires et surprenantes aventures, embarquez pour un voyage au coeur de lâastronomie babylonienne, des papyrus grecs, des manuscrits arabes et latins et des premiÃĻres inscriptions mayas.
Le zÃĐro a ÃĐtÃĐ inventÃĐ, oubliÃĐ, rÃĐinventÃĐ, transmis, traduit, repensÃĐ. Le spÃĐcialiste de lâhistoire des mathÃĐmatiques Antoine Houlou-Garcia nous raconte cet incroyable cheminement et toute lâintelligence humaine dâune science sans frontiÃĻres.
Bienvenue dans lâhistoire dâun rien qui a tout changÃĐ !
(lien rÃĐmunÃĐrÃĐ par Amazon)
lu 859 fois
mercredi 14 juin 2023
Par Didier MÞller, mercredi 14 juin 2023 à 06:55 - Histoire des maths
lu 984 fois
mardi 13 juin 2023
Par Didier MÞller, mardi 13 juin 2023 à 06:55 - Jeux / ThÃĐorie des jeux
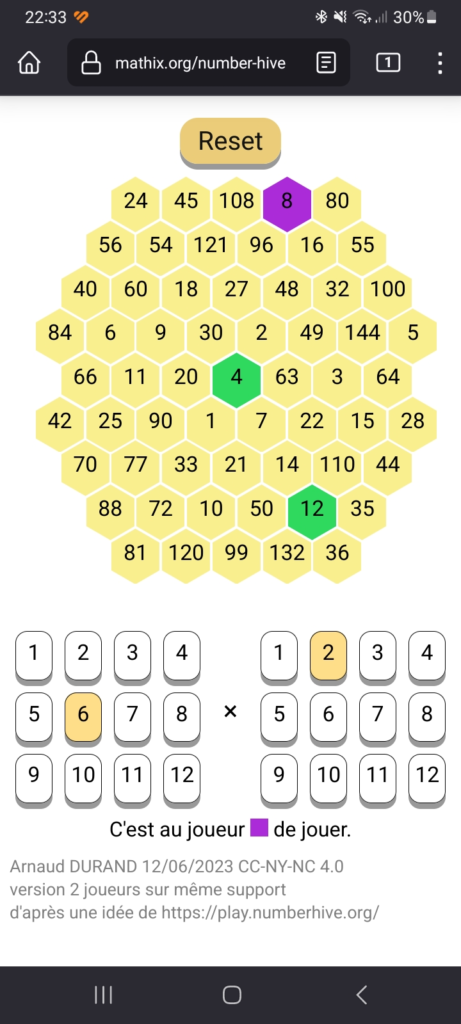
Number Hive est un jeu à deux qui permet d'exercer les multiplications de maniÃĻre ludique.
IdÃĐal pour finir l'annÃĐe scolaire!
Il se joue sur une ruche composÃĐe d'hexagones oÃđ figurent des nombres.
La rÃĻgle du jeu est simple :
lu 1197 fois
lundi 12 juin 2023
Par Didier MÞller, lundi 12 juin 2023 à 07:38 - DrÃīles de statistiques
lu 952 fois
dimanche 11 juin 2023
Par Didier MÞller, dimanche 11 juin 2023 à 21:53 - Voyages au pays des maths
lu 1037 fois
mardi 6 juin 2023
Par Didier MÞller, mardi 6 juin 2023 à 07:02 - Livres/e-books

La Guerre des nombres premiers
Maths, ÃĐco, crypto : ils sont sur tous les fronts
Yan Pradeau
Flammarion (31 mai 2023)
304 pages
PrÃĐsentation de l'ÃĐditeur
Briques ÃĐlÃĐmentaires des entiers, les nombres premiers irriguent tous les domaines des mathÃĐmatiques. Mais qui les a inventÃĐs ? Quel est le plus grand nombre premier connu ? Un ordre cachÃĐ gouverne-t-il leur distribution ? Et comment se rÃĐpartissent-ils parmi les entiers (une question à 1 million de dollars) ? Pour percer ces mystÃĻres, les mathÃĐmaticiens leur ont vouÃĐ une guerre acharnÃĐe, quand ils ne se sont pas affrontÃĐs par travaux interposÃĐs. L'enjeu est aussi ÃĐconomique - saviez-vous que les nombres premiers s'achÃĻtent ? -, ÃĐcologique - les calculs de primalitÃĐ consomment une ÃĐnergie colossale - et militaire - l'algorithme de cryptographie RSA à base de nombres premiers a ÃĐtÃĐ un temps interdit d'exportation par la NSA, l'Agence nationale de sÃĐcuritÃĐ amÃĐricaine. De coups tordus en batailles rangÃĐes, voici le rÃĐcit de cette passionnante guerre souterraine, de l'AntiquitÃĐ grecque jusqu'aux rÃĐcentes contributions de Terence Tao, en passant par les travaux de Mersenne, Fermat, Euler, Gauss et par l'hypothÃĻse de Riemann, "graal" des mathÃĐmatiques.
(lien rÃĐmunÃĐrÃĐ par Amazon)
lu 894 fois
vendredi 2 juin 2023
Par Didier MÞller, vendredi 2 juin 2023 à 06:37 - Il y a des maths là ?
MÊme sans sextant ni tÃĐlescope, on peut estimer (grossiÃĻrement) les distances des objets astronomiques dans le ciel. Il suffit de se servir de ses mains.
Lire l'article de Nelly Lesage sur Numerama
lu 896 fois
jeudi 1 juin 2023
Par Didier MÞller, jeudi 1 juin 2023 à 20:49 - Carnet noir
Le mathÃĐmaticien Pierre Audin est dÃĐcÃĐdÃĐ le 28 mai 2023 Ã l'ÃĒge de 66 ans.
Co-fondateur de MATh.en.JEANS, nous lui devons en grande partie le projet MeJ. Avec Pierre Duchet, ils ont crÃĐÃĐ le premier atelier en 1989, ils en ont ÃĐcrit les textes fondateurs et ils en ont fait diffuser l'idÃĐe (voir ici quelques textes).
Il voulait permettre lâaccÃĻs à la culture scientifique au plus grand nombre, but qu'il poursuivait aussi comme mÃĐdiateur au Palais de la DÃĐcouverte et au travers de projets en AlgÃĐrie.
lu 933 fois
mercredi 31 mai 2023
Par Didier MÞller, mercredi 31 mai 2023 à 09:49 - Doc/sÃĐries/films/vidÃĐos
An infinite playlist est une playlist de la chaÃŪne Youtube PBS Infinite Series contenant des petits films dâune dizaine de minutes autour du thÃĻme de lâinfini (en anglais).
lu 887 fois
vendredi 26 mai 2023
Par Didier MÞller, vendredi 26 mai 2023 à 06:53 - Illusions
the movement of the splits make this illusion work the circles are not actually spinning
by u/letitbesb in woahdude
lu 973 fois
jeudi 25 mai 2023
Par Didier MÞller, jeudi 25 mai 2023 à 07:33 - Cryptographie
Quelles seraient selon vous vos rÃĐactions et celles de la communautÃĐ scientifique autour du programme Seti à la suite de la dÃĐtection d'un message en provenance d'une civilisation extraterrestre avancÃĐe ? Le projet A Sign in Space va vous donner l'occasion de le savoir en simulant cet ÃĐvÃĐnement et en ouvrant mÊme l'analyse et l'interprÃĐtation de ce message à tous les membres de la noosphÃĻre sur le Web. L'arrivÃĐe du Message, c'est ce 24 mai 2023 au soir et aprÃĻs tout qui nous dit qu'il s'agit vraiment d'une simulation et pas d'une maniÃĻre de nous annoncer en douceur que nous avons bel et bien captÃĐ un message E.T ?
Lire l'article de Laurent Sacco sur Futura
Aller sur le site asignin.space
lu 866 fois
mardi 23 mai 2023
Par Didier MÞller, mardi 23 mai 2023 à 08:11 - Illusions
lu 1182 fois
lundi 22 mai 2023
Par Didier MÞller, lundi 22 mai 2023 à 07:38 - Il y a des maths là ?
Bir parça geometri bilgisiyle... pic.twitter.com/zkhVXQigO7
— Pratik DÞnya (@pratikdunya) May 20, 2023
lu 909 fois
dimanche 21 mai 2023
Par Didier MÞller, dimanche 21 mai 2023 à 08:26 - Illusions
Kokichi Sugihara, professeur d'ingÃĐnierie à l'UniversitÃĐ Meiji, a remportÃĐ le prix de la meilleure illusion de l'annÃĐe 2020 avec son escalier SchrÃķder 3D. Comme son homologue 2D, la version 3D a le mÊme aspect de face et de dos, semblant toujours descendre.
lu 895 fois
< 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 221 222 223 224 225 226 227 228 229 230 231 232 233 234 >