vendredi 15 dĂŠcembre 2023
Par Didier MĂźller,
vendredi 15 dĂŠcembre 2023 à 13:27
- Enigmes/casse-tĂŞte
Le Service GÊnÊral du Renseignement et de la SÊcuritÊ (SGRS) et le Ministère de la DÊfense de Belgique emploient en leur sein des agents aux capacitÊs d'analyse et de dÊduction au-dessus de la moyenne. Depuis 2018, certains de ces agents ont pris l'habitude de confronter les amateurs d'Ênigmes et de casse-tête à un puzzle de fin d'annÊe, publiÊ courant novembre et comportant plusieurs dizaines d'Ênigmes parfois très corsÊes. Les participants ont alors quelques semaines pour tenter de percer les mystères du puzzle avant d'envoyer leurs rÊponses à une date fixÊe. Des points sont attribuÊs à chacun en fonction de ses bonnes rÊponses, et un classement honorifique est publiÊ. Pas de rÊcompense à la clÊ, juste le challenge de se frotter à des concepteurs particulièrement brillants et de toucher du doigt les capacitÊs analytiques attendues pour un agent de la DÊfense et de la SÊcuritÊ.
Voir le concours 2022 au format pdf (je n'ai pas trouvĂŠ l'ĂŠdition 2023)
Voir les autres annĂŠes
lu 1022 fois
vendredi 1 dĂŠcembre 2023
Par Didier MĂźller,
vendredi 1 dĂŠcembre 2023 à 08:00
- Enigmes/casse-tĂŞte
ProposÊ par l'association Les Maths en Scène, sur une idÊe de Houria Lafrance, Le calendrier de l'Avent propose de rÊsoudre chaque jour une Ênigme pour ouvrir la case et dÊcouvrir la surprise.
lu 1105 fois
lundi 6 novembre 2023
Par Didier MĂźller,
lundi 6 novembre 2023 à 15:25
- Enigmes/casse-tĂŞte
En explorant le Figaro du 9 mars 1896, je suis tombÊ sur ce problème :


lu 839 fois
mardi 18 avril 2023
Par Didier MĂźller,
mardi 18 avril 2023 à 08:42
- Enigmes/casse-tĂŞte
43'252'003'274'489'856'000 (comment prononce-t-on ce nombre ?)

lu 1122 fois
mercredi 5 avril 2023
Par Didier MĂźller,
mercredi 5 avril 2023 à 16:34
- Enigmes/casse-tĂŞte
lu 912 fois
mercredi 22 fĂŠvrier 2023
Par Didier MĂźller,
mercredi 22 fĂŠvrier 2023 à 08:09
- Enigmes/casse-tĂŞte
La lÊgende raconte que quand quelqu'un demandait son âge au mathÊmaticien britannique Augustus de Morgan, il rÊpondait par l'Ênigme suivante: " J'avais x annÊes en l'an x² ".
En quelle annĂŠe est-il nĂŠ ?
lu 944 fois
mardi 14 fĂŠvrier 2023
Par Didier MĂźller,
mardi 14 fĂŠvrier 2023 à 11:16
- Enigmes/casse-tĂŞte
lu 966 fois
jeudi 5 janvier 2023
Par Didier MĂźller,
jeudi 5 janvier 2023 à 09:33
- Enigmes/casse-tĂŞte
Une expression pandigitale utilise tous les chiffres de 1 Ă 9. David DraĂŻ m'en a envoyĂŠ un certain nombre dont le rĂŠsultat est 2023 :
(đ + đ Ă đ) Ă ((đ â đ + đ) Ă đ Ă đ + đ) = đ Ă đđđ = đđđđ
(đ + đ + đ + đ Ă đ Ă đ â đ) Ă (đ + đ) = đđđ Ă đđ = đđđđ
(đ Ă đ Ă đ Ă đ Ă đ + đ â đ) Ă (đ + đ) = đđđ Ă đđ = đđđđ
đ + đ Ă đ Ă ((đ + đ Ă đ + đ) Ă đ + đ) = đ + đđđđ = đđđđ
đ + đ Ă đ Ă ((đ â đ + đ Ă đ) Ă đ + đ) = đ + đđđđ = đđđđ
(đ â đ + đ + đ + đ + đ) Ă đ Ă (đ + đ) = đđ Ă đ Ă đđ = đđđđ
đ + đ Ă đ â đ Ă (đ â đ) Ă đ Ă đ Ă đ = đ + đđđđ = đđđđ
(đ â đ Ă đ Ă đ Ă đ) Ă ((đ â đ) Ă đ â đ) = âđđđ Ă (âđđ) = đđđđ
đ + (đ â đ + đ) Ă (đ + đđđ â đ) = đ + đđđđ = đđđđ
đ + đ Ă đ Ă (đđđ â đ Ă (đ + đ)) = đ + đđđđ = đđđđ
(đ + đ + đđđ) Ă đ + đ â đ Ă đ = đđđđ â đđ = đđđđ
(đđđ â đ) Ă (đ + đ + đ + đ â đ) = đđđ Ă đđ = đđđđ
(đ + đ Ă đ) Ă (đ Ă đđ â đ + đ Ă đ) = đ Ă đđđ = đđđđ
(đ + đ Ă đ) Ă (đ Ă đđ + đ Ă đ + đ) = đ Ă đđđ = đđđđ
(đ + đ Ă đ) Ă (đ Ă (đ + đđ) â đ + đ) = đ Ă đđđ = đđđđ
(đ + đ Ă đ) Ă ((đ + đ) Ă đ Ă đ â đđ) = đ Ă đđđ = đđđđ
(đ + đ Ă (đ Ă đ â đ + đ) Ă đ Ă đ + đ = đđđđ + đ = đđđđ
(đ + đ Ă (đ + đ Ă đ + đ) Ă đ Ă đ + đ = đđđđ + đ = đđđđ
(đ + đ) Ă đ Ă ((đ â đ + đ) Ă đ + đ Ă đ = đđ Ă đ Ă đđ = đđđđ
đ Ă đ Ă (đ + đ) + đđđ Ă đ + đ = đđđđ + đ = đđđđ
(đ + đ Ă đ Ă (đ â đ + đ) Ă (đ Ă đ + đ) = đđđ Ă đ = đđđđ
(đ + đ) Ă ((đđ â đ â đ Ă đ) Ă đ + đ = đđ Ă đđđ = đđđđ
(đ + đ) Ă ((đđ â đ Ă đ + đ) Ă đ + đ = đđ Ă đđđ = đđđđ
(đ + đ) Ă ((đ + đđ â đ Ă đ) Ă đ â đ) = đđ Ă đđđ = đđđđ
(đ + đ) Ă đ Ă ((đ + đđ) á đ â đ â đ) = đđ Ă đ Ă đđ = đđđđ
(đ + đ) Ă (đ Ă (đ + đ) + đđ â đ + đ) = đđ Ă đđđ = đđđđ
(đ + đ) Ă đ Ă (đ â đ Ă đ + đđ â đ) = đđ Ă đ Ă đđ = đđđđ
(đ + đ) Ă (đ Ă đ + đ â đ Ă (đ â đđ) = đđ Ă đđđ = đđđđ
(đ â đ + (đ + đđ) Ă đ) Ă (đ Ă đ + đ) = đđđ Ă đ = đđđđ
lu 950 fois
dimanche 1 janvier 2023
Par Didier MĂźller,
dimanche 1 janvier 2023 à 11:08
- Enigmes/casse-tĂŞte
Trouvez la formule la plus courte permettant de calculer 2023 en ĂŠcrivant, dans l'ordre, les premiers nombres entiers, sĂŠparĂŠs par des opĂŠrateurs (+, -, *, /, racines carrĂŠes, exposants, factorielle).
Les Kitano de 2023 trouvĂŠs par Alain Zalmanski :
2023 = 1*2+(3!)^4+5+6!
2023 = (1+2+3)^4+(5!)*6+7
2023 = (((1+2)^3+4)*5)*(6+7)+8
2023 = ((1+2+3-4)*56+7)*(8+9)
lu 942 fois
lundi 26 septembre 2022
Par Didier MĂźller,
lundi 26 septembre 2022 à 07:27
- Enigmes/casse-tĂŞte
Combien faut-il de cavaliers pour contrĂ´ler ou occuper toutes les cases d'un ĂŠchiquier 8x8 ? (et comment les placer ?)
RĂŠponse ici.
lu 956 fois
jeudi 22 septembre 2022
Par Didier MĂźller,
jeudi 22 septembre 2022 à 22:05
- Enigmes/casse-tĂŞte
Vous avez un verre en main et vous vous trouvez devant un immeuble de 100 ĂŠtages. Vous vous demandez alors :
"A partir de quel ĂŠtage le verre jetĂŠ de la fenĂŞtre se cassera-t-il ?"
Si vous ne pouvez sacrifier quâun seul verre, la seule stratĂŠgie est de tester les ĂŠtages un par un, en remontant. Votre ami qui lui aussi a un verre en main vous propose son verre pour accĂŠlĂŠrer lâexpĂŠrience. Le jeu consiste alors Ă trouver une stratĂŠgie qui donne le nombre minimal de lancers, pour rĂŠpondre Ă la question de façon certaine (en cassant au plus 2 verres) dans tous les cas. Effectivement, on peut gagner beaucoup dâessais grâce au second verre. Par exemple, on peut jeter un verre du cinquantième ĂŠtage et nâavoir alors plus quâau plus 50 ĂŠtages Ă tester. Cela donne alors une solution en moins de 51 lancers (la pire des situations ĂŠtant celle oĂš le verre ne casse mĂŞme pas du 100 ème ĂŠtage). Mais il y a bien mieux ! Lancer le premier verre au 10 ème, puis au 20 ème sâil ne se casse pas, et ainsi de suite de 10 en 10. Puis dès quâil se casse, on utilise le second pour affiner la fourchette dans lâintervalle dĂŠterminĂŠ en testant au plus 9 ĂŠtages intermĂŠdiaires. Cela fait au plus 19 lancers ! On a lâimpression que les stratĂŠgies vont dĂŠpendre de lâarithmĂŠtique de ce nombre dâĂŠtages.
RĂŠponse dans le billet de Sylvain BarrĂŠ sur Images des mathĂŠmatiques
lu 965 fois
mercredi 13 juillet 2022
Par Didier MĂźller,
mercredi 13 juillet 2022 à 18:07
- Enigmes/casse-tĂŞte
ABCD + A + B + C + D = 1991.
Trouver A, B, C et D en raisonnant (sans ordinateur).
Un exemple pour clarifier l'ĂŠnoncĂŠ : 2831 + 2 + 8 + 3 + 1 = 2845...
lu 957 fois
dimanche 29 mai 2022
Par Didier MĂźller,
dimanche 29 mai 2022 à 07:31
- Enigmes/casse-tĂŞte
Le problème du sofa est un problème mathÊmatique conceptuel formalisÊ par le mathÊmaticien Leo Moser en 19661. Il s'agit de trouver le sofa d'aire maximale que l'on peut dÊplacer horizontalement dans un couloir d'un mètre de large avec un angle droit.

Le problème n'est toujours pas rÊsolu...
Source : WikipĂŠdia
lu 1299 fois
vendredi 1 avril 2022
Par Didier MĂźller,
vendredi 1 avril 2022 à 14:12
- Enigmes/casse-tĂŞte
Aire bleue = ?
 Source : Daniel Mentrard
Source : Daniel Mentrard
lu 1113 fois
lundi 14 fĂŠvrier 2022
Par Didier MĂźller,
lundi 14 fĂŠvrier 2022 à 09:59
- Enigmes/casse-tĂŞte
lu 1066 fois
jeudi 10 fĂŠvrier 2022
Par Didier MĂźller,
jeudi 10 fĂŠvrier 2022 à 09:07
- Enigmes/casse-tĂŞte
Je suis fan des problèmes "Blue area?" de Daniel Mentrard...
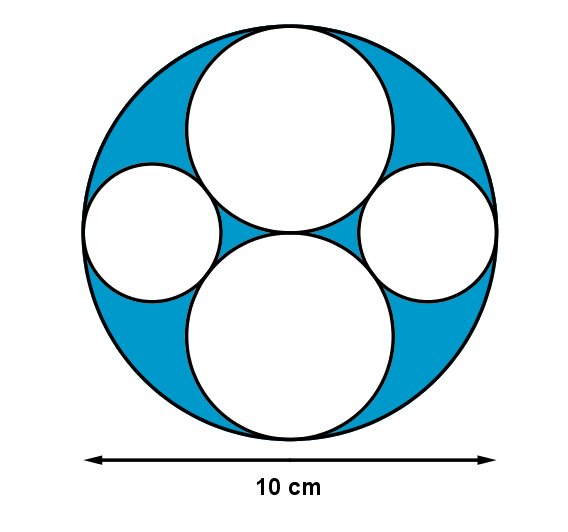
lu 1096 fois
mercredi 5 janvier 2022
Par Didier MĂźller,
mercredi 5 janvier 2022 à 07:19
- Enigmes/casse-tĂŞte
Trouvez la formule la plus courte permettant de calculer 2022 en ĂŠcrivant, dans l'ordre, les premiers nombres entiers, sĂŠparĂŠs par des opĂŠrateurs (+, -, *, /, racine carrĂŠe, exposant, factorielle).
J'en ai trouvĂŠ deux :
- (1+2) * ((3!)! - 4) - 5! - 6 = 2022
- (1+2)! + (3!)4 + 5! * 6 = 2022
lu 1116 fois
vendredi 24 dĂŠcembre 2021
Par Didier MĂźller,
vendredi 24 dĂŠcembre 2021 à 09:48
- Enigmes/casse-tĂŞte
Le GCHQ (Government Communications Headquarters) est le pendant britannique de la NSA amĂŠricaine. Il propose un dĂŠfi de NoĂŤl, Ă rĂŠsoudre en famille.

lu 1091 fois
dimanche 5 dĂŠcembre 2021
Par Didier MĂźller,
dimanche 5 dĂŠcembre 2021 à 07:53
- Enigmes/casse-tĂŞte
Ce Calendrier de l'Avent est proposÊ par l'association Les Maths en Scène sur une idÊe de Houria Lafrance.
Chaque jour, rÊsolvez une Ênigme pour ouvrir la case et dÊcouvrir la surprise. Certaines Ênigmes sont faciles, d'autres pas. Si vous ne trouvez pas la rÊponse, pas de problème : la case s'ouvrira toute seule trois jours après la date.
lu 1236 fois
samedi 16 octobre 2021
Par Didier MĂźller,
samedi 16 octobre 2021 à 10:26
- Enigmes/casse-tĂŞte
Le cĂŠlèbre mathĂŠmaticien indien Ramanujan composa le carrĂŠ magique ci-dessous, oĂš la somme des cases dâune mĂŞme couleur donne toujours 139.

De plus, la première ligne de ce carrÊ est sa date de naissance (22 DÊcembre 1887).
Source : AnecdotesMaths
lu 2407 fois
< 1 2 3 4 5 6 7 8 9 10 11 >








